Hostname: page-component-6dbcb7884d-2bcm2 Total loading time: 0 Render date: 2025-02-14T09:02:36.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic complexes. II

Published online by Cambridge University Press:  24 October 2008

P. E. Newstead
P. E. Newstead
Affiliation:
University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

A quadratic complex Q is the set of lines in 3-dimensional projective space 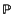3 given by a single non-trivial quadratic equation in the Plücker coordinates. The lines of the complex which pass through a fixed point of 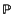3 are, in general, the generators of a quadric cone; this cone degenerates for the points of a sub variety K of 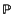3. Thus one can associate with Q a fibration with base 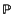3 - K and fibre isomorphic to 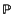1, and ask whether this fibration is associated with an algebraic vector bundle of rank 2. When the base field is 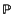and Q is non-singular, the answer is negative; this was proved some years ago by Narasimhan and Ramanan ((8), proposition 8·1), and has the consequence that there is no universal family of stable vector bundles of rank 2 and degree 0 over a curve of genus 2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 2 , March 1982 , pp. 183 - 206
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Desale, U. V. and Ramanan, S.Classification of vector bundles of rank 2 on hyperelliptic curves. Invent. Math. 38 (1976), 161–185.CrossRefGoogle Scholar
(2)Frobenius, G.Über die schiefe Invariante einer bilinearen oder quadratischen Form. J. Reine Angew. Math. (Crelle'e Journal) 86 (1879), 44–71.Google Scholar
(3)Hartshorne, R.Algebraic geometry (Springer-Verlag, 1977).Google Scholar
(4)Hodge, W. V. D. and Pedoe, D.Methods of algebraic geometry, vol. ii (Cambridge University Press, 1952).Google Scholar
(5)Jessop, C. M.A treatise on the line complex (Cambridge University Press, 1903).Google Scholar
(6)Klein, F.Über die Transformation der allgemeinen Gleichung des zweiten Grades zwischen Linien-Coordinaten auf eine canonische Form (Inauguraldissertation, Bonn, 1868), Math. Ann. 23 (1884), 539–578 (Gessammelte Math. Abh., Bd. i, 5–48).Google Scholar
(7)Narasimhan, M. S. and Ramanan, S.Moduli of vector bundles on a compact Riemann surface. Ann. of Math. 89 (1969), 14–51.CrossRefGoogle Scholar
(8)Narasimhan, M. S. and Ramanan, S. Vector bundles on curves. Algebraic geometry (papers presented at the Bombay Colloquium 1968), 335–346 (O.U.P., India, 1969).Google Scholar
(9)Newstead, P. E.Stable bundles of rank 2 and odd degree over a curve of genus 2. Topology 7 (1968), 205–215.CrossRefGoogle Scholar
(10)Newstead, P. E.A note on quadratic complexes. J. London Math. Soc. 5 (1972), 748–752.CrossRefGoogle Scholar
(11)Newstead, P. E.Comparison theorems for conic bundles. Math. Proc. Cambridge Phil. Soc., 90 (1981), 21–31.Google Scholar
(12)Ramanan, S. Orthogonal and spin bundles over hyperelliptic curves. Geometry and analysis (Papers dedicated to the memory of V. K. Patodi) (Bombay, 1980), 151–166.Google Scholar
(13)Reid, M. A. The complete intersection of two or more quadrics (Thesis, Cambridge University, 1972).Google Scholar
(14)Segre, C. ‘Studio sulle quadriche in uno spazio lineare ad un numero qualunque di dimensioni’ and ‘Sulla geometria della retta e delle sue serie quadratiche’. Mem. R. Accad. Torino 36 (1884).Google Scholar
(15)Shafarevich, I. R.Basic algebraic geometry (Springer-Verlag, 1974).Google Scholar
(16)Sturm, R.Die Gebilde ersten und zweiten Grades der Liniengeometrie in synthetischer Behandlung. III. Die Strahlencomplexe zweiten Grades. (Teubner, Leipzig, 1896).Google Scholar
(17)Weierstrass, K.Zur Theorie der bilinearen und quadratischen Formen. Monatsberichte der Berlin Acad. (1868), 310–338 (Mathematische Werke Bd. II, 19–44).Google Scholar
(18)Weiler, A.Über die verschiedenen Gattungen der Complexe zweiten Grades. Math. Ann. 7 (1874), 145–207.Google Scholar
(19)Zindler, K. Algebraischen Liniengeometrie. Encyklopädie der mathematischen Wissenschaften, Bd. III, 973–1228 (Teubner, Leipzig, 1921–1928).Google Scholar