Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Seeger, Andreas
Wainger, Stephen
and
Wright, James
1997.
Spherical Maximal Operators on Radial Functions.
Mathematische Nachrichten,
Vol. 187,
Issue. 1,
p.
241.
Duoandikoetxea, Javier
and
Vargas, Ana
1998.
Maximal operators associated to Fourier multipliers with an arbitrary set of parameters.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 4,
p.
683.
Havard, François
and
Lesigne, Emmanuel
2010.
Averages on annuli of Euclidean space.
Advances in Pure and Applied Mathematics,
Vol. 1,
Issue. 2,
Cho, Chu-Hee
Lee, Sanghyuk
and
Vargas, Ana
2012.
Problems on Pointwise Convergence of Solutions to the Schrödinger Equation.
Journal of Fourier Analysis and Applications,
Vol. 18,
Issue. 5,
p.
972.
Heo , Yaryong
2016.
Multi-Parameter Maximal Operators Associated with Finite Measures and Arbitrary Sets of Parameters.
Integral Equations and Operator Theory,
Vol. 86,
Issue. 2,
p.
185.
Hughes, Kevin
2017.
Restricted weak-type endpoint estimates for k-spherical maximal functions.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
1303.
Hughes, Kevin
2019.
The discrete spherical averages over a family of sparse sequences.
Journal d'Analyse Mathématique,
Vol. 138,
Issue. 1,
p.
1.
Guo, Shaoming
Roos, Joris
Seeger, Andreas
and
Yung, Po-Lam
2020.
Maximal functions associated with families of homogeneous curves: Lp bounds for P ≤ 2.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 2,
p.
398.
Dimou, Evangelos
and
Seeger, Andreas
2020.
ON POINTWISE CONVERGENCE OF SCHRÖDINGER MEANS.
Mathematika,
Vol. 66,
Issue. 2,
p.
356.
Anderson, T.
Hughes, K.
Roos, J.
and
Seeger, A.
2021.
$$\mathbf {L^p\rightarrow L^q}$$ bounds for spherical maximal operators.
Mathematische Zeitschrift,
Vol. 297,
Issue. 3-4,
p.
1057.
Cho, Chu-Hee
Ko, Hyerim
Koh, Youngwoo
and
Lee, Sanghyuk
2023.
Pointwise convergence of sequential Schrödinger means.
Journal of Inequalities and Applications,
Vol. 2023,
Issue. 1,
Beltran, David
Roos, Joris
and
Seeger, Andreas
2024.
Multi-scale Sparse Domination.
Memoirs of the American Mathematical Society,
Vol. 298,
Issue. 1491,
Borges, Tainara
and
Foster, Benjamin
2024.
Bounds for Lacunary Bilinear Spherical and Triangle Maximal Functions.
Journal of Fourier Analysis and Applications,
Vol. 30,
Issue. 5,
Ryu, Jaehyeon
and
Seeger, Andreas
2024.
Spherical maximal functions on two step nilpotent Lie groups.
Advances in Mathematics,
Vol. 453,
Issue. ,
p.
109846.
Borges, Tainara
Foster, Benjamin
and
Ou, Yumeng
2025.
Sobolev smoothing estimates for bilinear maximal operators with fractal dilation sets.
Journal of Functional Analysis,
Vol. 288,
Issue. 2,
p.
110694.


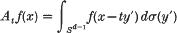
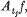 , for any particular sequence
, for any particular sequence 