No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let (X1, …, Xn) be the coordinates of the centre of a unit cube C, in n-dimensional space, whose (n − 1)-dimensional faces are parallel to the axes of coordinates. Further let the X's be integers. Let εi = ± 1 for r (≤ n) values of i, 1 ≤ i ≤ n, and let εi = 0 for the remaining n − r values of i. Then (X1 + ε1, …, Xn + εn) gives the centre of a cube C′, which touches the cube C along an (n − r)-dimensional edge or face. The cube C and the cubes C′, for all possible arrangements of the ε's, which are subject to the above conditions, form a symmetrical arrangement of 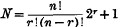 cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.
cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.