Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T02:43:35.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonal pairs of weak*-closed inner ideals in a JBW*-triple

Published online by Cambridge University Press:  01 July 2007

C. MARTIN EDWARDS
C. MARTIN EDWARDS*
Affiliation:
The Queen's College, Oxford, OX1 4AW.
Get access Rights & Permissions [Opens in a new window]

Abstract

Pre-symmetric complex Banach spaces have been proposed as models for state spaces of physical systems. A neutral GL-projection on a pre-symmetric space represents an operation on the corresponding system, and has as its range a further pre-symmetric space which represents the state space of the resulting system. Two neutral GL-projections S and T on the pre-symmetric space A* are said to be L-orthogonal if for all elements x in SA* and y in TA*,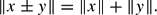By studying the algebraic properties of the dual space A of A*, which is a JBW*-triple, it is shown that, provided that the orthogonal neutral GL-projections S and T satisfy a certain geometrical condition, there exists a smallest neutral GL-projection S∨T majorizing both S and T, and that S, T and S∨T form a compatible family.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 1 , July 2007 , pp. 121 - 144
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alfsen, E. M. and Effros, E. G.. Structure in real Banach spaces I. Ann. Math. 96 (1972), 98–128.CrossRefGoogle Scholar
[2]Alfsen, E. M. and Effros, E. G.. Structure in real Banach spaces II. Ann. Math. 96 (1972), 129–174.CrossRefGoogle Scholar
[3]Barton, T. J. and Timoney, R. M.. Weak*-continuity of Jordan triple products and its applications. Math. Scand. 59 (1986), 177–191.CrossRefGoogle Scholar
[4]Barton, T. J., Dang, T. and Horn, G.. Normal representations of Banach Jordan triple systems. Proc. Amer. Math. Soc. 102 (1987), 551–555.CrossRefGoogle Scholar
[5]Behrends, E.. M-Structure and the Banach-Stone Theorem. Lecture Notes in Math. 736 (Springer–Verlag, 1979).CrossRefGoogle Scholar
[6]Bonsall, F. F. and Duncan, J.. Numerical Ranges of Operators on Normed Spaces and of Elements of Normed Algebras (Cambridge University Press, 1971).CrossRefGoogle Scholar
[7]Bunce, L. J. and C-H. Chu. Compact operations, multipliers and the Radon Nikodym property in JB*-triples. Pacific J. Math. 153 (1992), 249–265.CrossRefGoogle Scholar
[8] F. Cunningham Jnr. M-structure in Banach spaces. Math. Proc. Camb. Phil. Soc. 63 (1967), 613–629.CrossRefGoogle Scholar
[9]Cunningham Jnr., F., Effros, E. G. and Roy, N. M.. M-structure in dual Banach spaces. Israel J. Math. 14 (1973), 304–309.CrossRefGoogle Scholar
[10]Dineen, S.. Complete holomorphic vector fields in the second dual of a Banach space. Math. Scand. 59 (1986), 131–142.CrossRefGoogle Scholar
[11]Dineen, S.. The second dual of a JB*-triple syste. In Complex Analysis, Functional Analysis and Approximation Theory, (Mujica, J., Ed.) (North Holland, 1986).Google Scholar
[12]Edwards, C. M.. On Jordan W*-algebras. Bull. Sci. Math. 104 (1980), 393–403.Google Scholar
[13]Edwards, C. M.. The structure of Peirce inner ideals in JBW*-triples. Math. Proc. Camb. Phil. Soc. 136 (2004), 213–238.CrossRefGoogle Scholar
[14]Edwards, C. M. and V, R.. Hügli. Order structure of the set of GL-projections on a complex Banach space. Atti Sem. Mat. Fis. Univ. Modena. 53 (2005), 271–287.Google Scholar
[15]Edwards, C. M., Hügli, R. V. and Rüttimann, G. T.. A geometric characterization of structural projections on a JBW*-triple. J. Funct. Anal. 202 (2003), 174–194.CrossRefGoogle Scholar
[16]Edwards, C. M., Lörch, D. and Rüttimann, G. T.. Compatible subtriples of Jordan *-triples. J. Algebra 216 (1999), 707–740.CrossRefGoogle Scholar
[17]Edwards, C. M., McCrimmon, K. and T, G.. Rüttimann. The range of a structural projection. J. Funct. Anal. 139 (1996), 196–224.CrossRefGoogle Scholar
[18]Edwards, C. M. and T, G.. Rüttimann. Inner ideals in W*-algebras. Michigan Math. J. 36 (1989), 147–159.CrossRefGoogle Scholar
[19]Edwards, C. M. and G. T. Rüttimann. A characterization of inner ideals in JB*-triples. Proc. Amer. Math. Soc. 116 (1992), 1049–1057.Google Scholar
[20]Edwards, C. M. and G. T. Rüttimann. Structural projections on JBW*-triples. J. London Math. Soc. 53 (1996), 354–368.CrossRefGoogle Scholar
[21]Edwards, C. M. and Rüttimann, G. T.. Peirce inner ideals in Jordan *-triples. J. Algebra 180 (1996), 41–66.CrossRefGoogle Scholar
[22]Edwards, C. M. and G. T. Rüttimann. The lattice of weak*-closed inner ideals in a W*-algebra. Commun. Maths. Phys. 197 (1998), 131–166.CrossRefGoogle Scholar
[23]Edwards, C. M. and G. T. Rüttimann. Gleason's Theorem for rectangular JBW* triples. Commun. Math. Phys. 203 (1999), 269–295.CrossRefGoogle Scholar
[24]Edwards, C. M. and G. T. Rüttimann. The centroid of a weak*-closed inner ideal in a JBW*-triple. Archiv der Math. 76 (2001), 299–307.CrossRefGoogle Scholar
[25]Edwards, C. M. and G. T. Rüttimann. Faithful inner ideals in JBW*-triples. Result. Math. 43 (2003), 245–269.CrossRefGoogle Scholar
[26]Edwards, C. M. and G. T. Rüttimann. Involutive and Peirce gradings in JBW*-triples. Comm. Algebra 31 (2003), 2819–2848.CrossRefGoogle Scholar
[27]Friedman, Y.. Bounded symmetric domains and the JB*-structure in physics. In Jordan Algebras (Oberwolfach, 1992), (de Gruyter, 1994).Google Scholar
[28]Friedman, Y.. Physical Applications of Homogeneous Balls (Birkhäuser, 2005).CrossRefGoogle Scholar
[29]Friedman, Y. and Gofman, Y.. Why does the geometric product simplify the equations of physics? Internat. J. Theoret. Phys. 41 (2002), 1841–1855.CrossRefGoogle Scholar
[30]Friedman, Y. and Gofman, Y.. Relativistic spacetime transformations based on symmetry. Found. Phys. 32 (2002), 1717–1736.CrossRefGoogle Scholar
[31]Friedman, Y. and Russo, B.. Structure of the predual of a JBW*-triple. J. Reine Angew. Math. 356 (1985), 67–89.Google Scholar
[32] H. Hanche–Olsen and E. Størmer. Jordan Operator Algebras (Pitman, 1984).Google Scholar
[33]Harris, L. A.. Bounded symmetric domains in infinite-dimensional spaces. In Proceedings on Infinite-Dimensional Holomorphy (Hayden, T. L. and Suffridge, T. J., Eds.). Lecture Notes in Math. 364 (Springer–Verlag, 1974).CrossRefGoogle Scholar
[34]Horn, G.. Characterization of the predual and the ideal structure of a JBW*-triple. Math. Scand. 61 (1987), 117–133.CrossRefGoogle Scholar
[35]Kaup, W.. Riemann mapping theorem for bounded symmetric domains in complex Banach spaces. Math. Z. 183 (1983), 503–529.CrossRefGoogle Scholar
[36]Kaup, W.. Contractive projections on Jordan C*-algebras and generalizations. Math. Scand. 54 (1984), 95–100.CrossRefGoogle Scholar
[37]Loos, O.. Jordan Pairs. Lecture Notes in Math. 460 (Springer–Verlag, 1975).CrossRefGoogle Scholar
[38]Loos, O.. On the socle of a Jordan pair. Collect. Math. 40 (1989), 109–125.Google Scholar
[39]Pedersen, G. K.. C*-Algebras and their Automorphism Groups. London Math. Soc. Monogr. 14 (Academic Press, 1979).Google Scholar
[40]Sakai, S.. C*-Algebras and W*-Algebras (Springer–Verlag, 1971).Google Scholar
[41]L, L.. Stachó. A projection principle concerning biholomorphic automorphisms. Acta Sci. Math. 44 (1982), 99–124.Google Scholar
[42]Upmeier, H.. Symmetric Banach Manifolds and Jordan C*-Algebras (North Holland, 1985).Google Scholar
[43]Upmeier, H.. Jordan Algebras in Analysis, Operator theory and Quantum Mechanics (American Mathematical Society, 1986).Google Scholar
[44]Wright, J. D. M.. Jordan C*-algebras. Michigan Math. J. 24 (1977), 291–302.CrossRefGoogle Scholar
[45]Youngson, M. A.. A Vidav theorem for Banach Jordan algebras. Math. Proc. Camb. Phil. Soc. 84 (1978), 263–272.CrossRefGoogle Scholar