Article contents
On the method for solution of unsteady thermal boundary-layers in case of two-dimensional low-speed flows
Published online by Cambridge University Press: 24 October 2008
Abstract
This paper is dedicated to the question of solving unsteady thermal boundary-layers in the case of two-dimensional low-speed flows, provided that the difference between the temperature of the stream and that of the wall is not too great (so that the density is sensibly constant) and that the change in the wall temperature Tw (x, t) takes place at the same instant as the body is set into motion. The velocity boundary-layer is uncoupled from the thermal one and can be considered separately. In paper (2) is given the method for obtaining the velocity field (u, v). The temperature field T depends on the velocity field and can be obtained only after this one. The method (2) being available for this purpose assuming the difference between the temperature of the wall Tw (x, t) and that of the main-stream T∞ in the form of
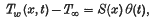
where S(x) and θ(t) are arbitrary functions of x respectively t, satisfying certain conditions required by the method.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 3 , July 1968 , pp. 849 - 870
- Copyright
- Copyright © Cambridge Philosophical Society 1968
References
REFERENCES
- 1
- Cited by


