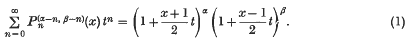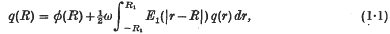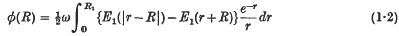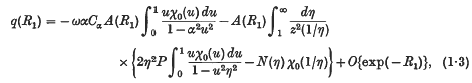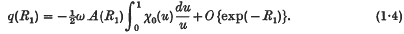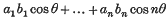Research Article
A problem of bounded expressibility in free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 573-584
-
- Article
- Export citation
A characterization of sets of n points which determine n hyperplanes†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 585-588
-
- Article
- Export citation
Subplanes of the Hughes plane of order 9
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 589-598
-
- Article
- Export citation
A group with zero homology
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 599-602
-
- Article
- Export citation
An algorithm for the construction of 3-manifolds from 2-complexes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 603-614
-
- Article
- Export citation
Uniform approximation by Fourier–Stieltjes coefficients
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 615-624
-
- Article
- Export citation
Stable subspaces of L1 + L∞
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 625-644
-
- Article
- Export citation
An inner measure associated with a von Neumann algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 645-650
-
- Article
- Export citation
On a class of functions regular in the unit disc
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 651-654
-
- Article
- Export citation
Cubic polynomials with the same residues (mod p)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 655-658
-
- Article
- Export citation
Arithmetic on curves with complex multiplication by √ − 2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 659-672
-
- Article
- Export citation
Sums of three roots of unity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 673-682
-
- Article
- Export citation
A note on the real zeros of the basic confluent hypergeometric function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 683-686
-
- Article
- Export citation
Bilinear and trilinear generating functions for Jacobi polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 687-690
-
- Article
- Export citation
Some new generating functions for Jacobi polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 691-694
-
- Article
- Export citation
A probabilistic proof of a formula for Jacobi polynomials by L. Carlitz
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 695-698
-
- Article
- Export citation
Expansions in series of Gontcharoff polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 699-703
-
- Article
- Export citation
A simple method of summing Bessel series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 705-710
-
- Article
- Export citation
Note on the isotropic scattering of radiation from a point source in a finite spherical atmosphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 711-719
-
- Article
- Export citation
The average number of real zeros of a random trigonometric polynomial
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 721-730
-
- Article
- Export citation

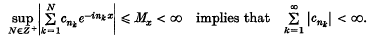
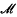 is constructed on the linear sets of a Hilbert space. We supposed
is constructed on the linear sets of a Hilbert space. We supposed 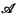 with a dense set of asymptotic values on {|
with a dense set of asymptotic values on {|
 is defined as ((5), p. 255)
is defined as ((5), p. 255)
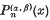 be the Jacobi polynomial as defined by Szegö in (7) (see equation (4) below.) Carlitz in (2) presented among others the following formula
be the Jacobi polynomial as defined by Szegö in (7) (see equation (4) below.) Carlitz in (2) presented among others the following formula