Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T02:18:04.556Z Has data issue: false hasContentIssue false
  • English
  • Français

On the converse of absolute Abel summability

Published online by Cambridge University Press:  24 October 2008

B. Kwee
B. Kwee
Affiliation:
University of Malaya, Kuala Lumpur
Get access Rights & Permissions [Opens in a new window]

Extract

The series 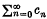is said to be summable A to s if the power series 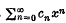converges to φ(x) for 0 ⋞ x < 1 and limx→1 φ(x) = s. If the function ⋞(x) is of bounded variation over the same interval, the series is said to be summable │A│. It is easy to prove │A│ ⊆ A, i.e. a series summable │A│ is necessarily summable A to the same sum.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 3 , May 1982 , pp. 453 - 456
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Agnew, R. P.Math. Reviews 20 (1959), 1141.Google Scholar
(2)Kien-Kwong, Chen.Convergence of absolutely summable series. Scientia Sinica 4 (1955), 211–228.Google Scholar
(3)Kien-Kwong, Chen.The absolute summability A of infinite series (Chinese with English summary). Acta Math. Sinica 6 (1956), 170–183.Google Scholar
(4)Fekete, M.On the absolute summability (A) of infinite series. Proc. Edinburgh Math. Soc. (2), 3 (1933), 132–134.Google Scholar
(5)Hardy, G. H.Theorems relating to the summability and convergence of slowly oscillating series. Proc. London Math. Soc. (2), 8 (1910), 301–320.CrossRefGoogle Scholar
(6)Littlewood, J. E.The converse of Abel's theorem on power series. Proc. London Math. Soc. (2), 9 (1910), 434–448.Google Scholar