Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T03:06:05.683Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Brunn-Minkowski coefficient of a locally compact unimodular group

Published online by Cambridge University Press:  24 October 2008

M. McCrudden
M. McCrudden
Affiliation:
Birmingham University
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a locally compact topological group, and let μ be the left Haar measure on G, with μ the corresponding outer measure. If R' denotes the non-negative extended real numbers, B (G) the Borel subsets of G, and V = {μ(C):C ∈ B(G)}, then we can define ΦG: V × V → R' by

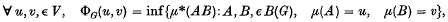
where AB denotes the product set of A and B in G. Then clearly

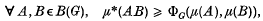
so that a knowledge of ΦG will give us some idea of how the outer measure of the product set AB compares with the measures of the sets A and B.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 1 , January 1969 , pp. 33 - 45
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ambrose, W.Direct sum theorem for Haar measures. Trans. Amer. Math. Soc. 71 (1947), 122–127.Google Scholar
(2)Halmos, P.Measure Theory (New York, 1950).CrossRefGoogle Scholar
(3)Henstock, R. and Macbeath, A. M.On the measure of sum-sets, 1. Proc. London Math. Soc. 3, (1953), 182–194.Google Scholar
(4)Iwasawa, K.On some types of topologioal groups. Ann. of Math. 50 (1949), 507–558.CrossRefGoogle Scholar
(5)Kemperman, J. H. B.On product sets in a locally compact group. Fund. Math. 56 (1964), 51–68.Google Scholar
(6)Kneser, M.Summenmengen in lokalkompakten Abelschen Gruppen. Math. Z. 66 (1956), 88–110.Google Scholar
(7)Macbeath, A. M.On the measure of product sets in a topological group. J. London Math. Soc. 35 (1960), 403–407.CrossRefGoogle Scholar
(8)Montgomery, D. and Zippin, L.Topological Transformation Groups (New York, 1955).Google Scholar
(9)Nachbin, L.The Haar Integral (New York, 1965).Google Scholar