Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T14:35:43.344Z Has data issue: false hasContentIssue false
  • English
  • Français

On representing sets of an almost disjoint family of sets

Published online by Cambridge University Press:  24 October 2008

P. Komjath  and
E. C. Milner
P. Komjath
Affiliation:
R. Eötvös University, Budapest 1775, Hungary
E. C. Milner
Affiliation:
University of Calgary, Calgary, Alta. T2N 1N4, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

For cardinal numbers λ, K, ∑ a (λ, K)-family is a family of sets such that || = and |A| = K for every A ε , and a (λ, K, ∑)-family is a (λ,K)-family such that |∪| = ∑. Two sets A, B are said to be almost disjoint if

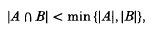
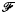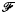and an almost disjoint family of sets is a family whose members are pairwise almost disjoint. A representing set of a family is a set X ⊆ ∪ such that X ∩ A = ⊘ for each A ε . If is a family of sets and |∪| = ∑, then we write εADR() to signify that is an almost disjoint family of ∑-sized representing sets of . Also, we define a cardinal number

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 3 , May 1987 , pp. 385 - 393
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balanda, K. P.. Almost disjoint families of representing sets, Ph.D. Thesis, University of Queensland, 1982.Google Scholar
[2]Balanda, K. P.. Maximally almost disjoint families of representing sets. Math. Proc. Cambridge Philos. Soc. 93 (1983), 1–7.CrossRefGoogle Scholar
[3]Balanda, K. P.. Almost disjoint families of representing sets. Z. Math. Logik Grundlag. Math. 31 (1985), 71–77.CrossRefGoogle Scholar
[4]Erdös, P., Hajnal, A. and Milner, E. C.. On sets of almost disjoint subsets of a set. Acta Math. Acad. Sci. Hungar. 19 (1968), 209–218.CrossRefGoogle Scholar
[5]Erdös, P. and Hechler, S. H.. On maximal almost disjoint families over singular cardinals. In Infinite and Finite Sets (ed. Hajnal, A. et al. ), Colloq. Math. Janos Bolyai, vol. 10 (North-Holland, 1975), 597–604.Google Scholar
[6]Milner, E. C.. Transversals of disjoint sets. J. London Math. Soc. 43 (1968), 495–500.CrossRefGoogle Scholar
[7]Silver, J. H.. The independence of Kurepa's hypothesis and two cardinal conjectures in Model Theory. In Axiomatic Set Theory (ed. Scott, D. S.). Proc. Sympos. Pure Math., vol. 13, part 1 (Amer. Math. Soc., 1971), 383–390.CrossRefGoogle Scholar
[8]Tarski, A.. Sur la décomposition des ensembles en sous ensembles presque disjoints. Fund. Math. 12 (1928), 188–205 and 14 (1929), 205–215.CrossRefGoogle Scholar