Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T16:54:06.162Z Has data issue: false hasContentIssue false
  • English
  • Français

On ideals and sublattices in linear lattices and F-lattices

Published online by Cambridge University Press:  24 October 2008

Y. A. Abramovich  and
Z. Lipecki
Y. A. Abramovich
Affiliation:
Department of Mathematical Sciences, IUPUI, Indianapolis, IN 46205, U.S.A.
Z. Lipecki
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Wroclaw Branch, Kopernika 18, 51-617 Wroclaw, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

The main aim of this paper is to study the role of the assumptions in the following

Theorem 0. Every ideal I of codimension 1 in an F-lattice X is closed†.

For X a Banach lattice this result appears in [11], ii.5·3, corollary 3. The proof carries over to the case where X is an. F-lattice, i.e. a topological linear lattice the topology of which is metrizable and complete, with the help of a result due to Klee ([10], theorem v.5·5; see also [3], theorem 16·6). We first note that the assumption of metric completeness is essential (Example 2). We then extend Theorem 0 to the case of ideals of finite codimension (Theorem 1), and show that non-closed ideals exist whenever X is infinite-dimensional (Corollary 2). Our main result commenting on Theorem 0 is, however, the existence of dense sublattices of arbitrary codimension between 1 and 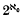in every infinite-dimensional F-lattice (Theorem 6).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 1 , July 1990 , pp. 79 - 87
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramovich, Y. A. and Lipecki, Z.. On lattices and algebras of simple functions. (Preprint.)Google Scholar
[2]Abramovich, Y. A., Lipecki, Z. and Rotkovich, G. Y.. One-codimensional dense sublattic of Banach lattices. Abstracts Amer. Math. Soc. 9 (1988). Abstract 88T–46–141, 334.Google Scholar
[3]Aliprantis, C. D. and Burkinshaw, O.. Locally Solid Riesz Spaces (Academic Press, 1978).Google Scholar
[4]Bhaskara Rao, K. P. S. and Bhaskara Rao, M.. Theory of Charges. A Study of Finitely Additive Measures (Academic Press, 1983).Google Scholar
[5]Drewnowski, L. and Lipecki, Z.. On some dense subspaces of topological linear spaces. II. Comment. Math. Prace Mat. 28 (1989), 175–188.Google Scholar
[6]Grätzer, G.. General Lattice Theory (Academic Press, 1978).CrossRefGoogle Scholar
[7]Lipecki, Z.. On some dense subspaces of topological linear spaces. Studia Math. 77 (1984 413–421.CrossRefGoogle Scholar
[8]Luxemburg, W. A. J. and Zaanen, A. C.. Riesz Spaces, vol. I (North-Holland, 1971).Google Scholar
[9]Mycielski, J.. Independent sets in topological algebras. Fund. Math. 55 (1964), 139–147).CrossRefGoogle Scholar
[10]Schaefer, H. H.. Topological Vector Spates (Macmillan, 1966).Google Scholar
[11]Schaefer, H. H.. Banach Lattices and Positive Operators (Springer-Verlag, 1974).CrossRefGoogle Scholar
[12]Yosida, K.. Functional Analysis (Springer-Verlag, 1965).Google Scholar