Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T14:18:14.739Z Has data issue: false hasContentIssue false
  • English
  • Français

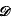On ( h(n)) summability methods

Published online by Cambridge University Press:  24 October 2008

B. Kuttner  and
I. L. Sukla
B. Kuttner
Affiliation:
University of Birmingham, U.K.
I. L. Sukla
Affiliation:
Department of Mathematics, Sambalpur University, Jyoti Vihar, Burla, 768019, Orissa, India
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1967 Segal introduced the Dirichlet convolution (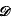, h(n)), generalizing a method of Ingham developed in studies on the Prime Number Theorem. In this paper we establish necessary and sufficient conditions on the sequence h(n) in order that the convolution method (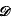, h(n)) be conservative. Further conditions are established for the method to be absolutely conservative.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 189 - 193
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooke, R. G.. Infinite Matrices and Sequence Spaces (Macmillan 1950, Dover 1955).Google Scholar
[2]Hardy, G. H.. Divergent Series (Oxford, 1949).Google Scholar
[3]Ingham, A. E.. Some Tauberian theorems connected with the Prime Number theorem. J. London Math. Soc. 20 (1945), 171–180.CrossRefGoogle Scholar
[4]Knopp, K. and Lorentz, G. G.. Beiträge zur absoluten Limitierung. Arch. Math. (Basel) 2 (1949), 10–16.CrossRefGoogle Scholar
[5]Segal, S. L.. Summability by Dirichlet convolution. Math. Proc. Cambridge Philos. Soc. 63 (1967), 393–400.CrossRefGoogle Scholar
[6]Segal, S. L.. Tauberian theorems for (, h(n)) summability. J. London Math. Soc. 44 (1969), 163–168.CrossRefGoogle Scholar