No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
If G is a group of finite order which contains an operation P of prime order p, permutable only with its own powers, the order of G must, by Sylow's theorem, be of the form (1 + kp) pś, where s is a factor of p – 1. The greatest subgroup of G, which contains self-conjugately {P};, the subgroup generated by P, must be a metacyclical subgroup {S, P}, where
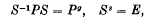
while g is a primitive root of the congruence gs = 1 (mod. p).
* Burnside, , Theory of Groups, § 221.Google Scholar
† Loc. cit. § 221.
‡ Loc., cit. § 234.
§ Loc. cit. § 218.
* Loc. cit. §§ 234, 235.
† Loc. cit. § 218.
* Loc. cit. § 219.
* Loc. cit. § 243.