Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T16:29:51.521Z Has data issue: false hasContentIssue false
  • English
  • Français

On characterizations of sphere-preserving maps

Published online by Cambridge University Press:  01 September 2009

BAOKUI LI  and
GUOWU YAO
BAOKUI LI
Affiliation:
Department of Mathematics, Beijing Institute of Technology, Beijing, 100081, China. e-mail: [email protected]
GUOWU YAO*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, China. e-mail: [email protected]
*
†Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, the first author and Y. Wang proved that 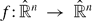(n ≥ 2) is a Möbius transformation if and only if f is a non-degenerate circle-preserving map. In this paper, we will further the result to show that f is a Möbius transformation if and only if f is a non-degenerate r–dimensional sphere-preserving map. The versions for the Euclidean and hyperbolic cases are also obtained. These results make no surjectivity or injectivity or even continuity assumptions on f. Moreover, certain degenerate sphere-preserving maps are given, which completes the characterizations of sphere-preserving maps.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 2 , September 2009 , pp. 439 - 446
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aczél, J. and McKiernan, M. A.On the characterization of hyperplane projective and complex Möbius-transformation. Math. Nachr. 33 (1967), 315–337.Google Scholar
[2]Beardon, A. F. and Minda, D.Sphere-preserving maps in inversive geometry. Proc. Amer. Math. Soc. 130 (2001), 987–998.CrossRefGoogle Scholar
[3]Chubarev, A. and Pinelis, I.Fundamental theorem of geometry without the 1-to-1 assumption. Proc. Amer. Math. Soc. 127 (1999), 2735–2744.Google Scholar
[4]Jeffers, J.Lost theorems of geometry. Amer. Math. Monthly. 107 (2000), 800–812.Google Scholar
[5]Li, B. and Wang, Y.Transformations and non-degenerate maps. Sci. China Ser. A, Mathematics. 48 Supp. (2005), 195–205.Google Scholar
[6]Nehari, Z.Conformal Mapping. (McGraw-Hill, 1952).Google Scholar
[7]Yao, G. W.On existence of degenerate circle-preserving maps. J. Math. Anal. Appl. 334 (2007), 950–953.Google Scholar
[8]Yao, G. W. Fundamental theorem of hyperbolic geometry without the injectivity assumption, to appear in Math. Nachr. available at http://arXiv.org-arXiv:0810.1580[math.CV].Google Scholar
[9]Yao, G. W. Transformations of spheres without the injectivity assumption. Preprint, 2008.Google Scholar