Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T01:44:24.507Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Gaussian process related to multivariate probability density estimation

Published online by Cambridge University Press:  24 October 2008

B. W. Silverman
B. W. Silverman
Affiliation:
Statistical Laboratory, University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The multivariate Gaussian process with the same variance/covariance structure as the multivariate kernel density estimator in Euclidean space of dimension d is considered. An exact result is obtained for the limit in probability of the maximum of the normalized process. In addition weak and strong bounds are placed on the asymptotic behaviour of the maximum of the process over a multidimensional interval which is allowed to increase as the sample size increases. All the bounds obtained on the process are

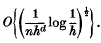
Only the uniform continuity of the underlying density is assumed; the conditions on the kernel are also mild.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 1 , July 1976 , pp. 135 - 144
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cramer, H. and Leadbetter, M. R.Stationary and related stochastic processes. (New York: J. Wiley & Sons, Inc., 1967.)Google Scholar
(2)Garsia, A. M. Continuity properties of Gaussian processes with multidimensional time parameter. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, volume II. (Berkeley: University of California Press, 1972), 369–374.Google Scholar
(3)Revesz, P. On multivariate empirical density functions. (To appear.)Google Scholar
(4)Rosenblatt, M.Remarks on some non-parametric estimates of a density function. Ann. Math. Statist. 27 (1956), 832–837.CrossRefGoogle Scholar
(5)Rosenblatt, M.A quadratic measure of deviation of two-dimensional density estimates and a test of independence. Ann. Statist. 3 (1975), 1–14.CrossRefGoogle Scholar