Note on the geometrical optics of diffracted wave fronts
Published online by Cambridge University Press: 24 October 2008
Extract
It is well known that a solution of the wave equation
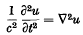
for which u = ∂u/∂t = 0 initially outside a surface S0, vanishes at time t in the exterior of a surface St parallel to, and at normal distance ct from S0, so that the wave fronts of disturbances represented by the solutions of the wave equation obey the laws of geometrical optics. Analogous results hold for the solutions of any linear hyperbolic second-order partial differential equation with boundary value conditions of the ‘Cauchy’ type. But the wave fronts of solutions of problems in which some of the boundary conditions are of the type representing reflexion do not seem to have been treated, and in particular the case of diffraction, when there is a ‘shadow’, does not seem to have been considered at all.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 3 , July 1949 , pp. 395 - 404
- Copyright
- Copyright © Cambridge Philosophical Society 1949
References
REFERENCES
- 8
- Cited by


