Hostname: page-component-6bf8c574d5-685pp Total loading time: 0 Render date: 2025-03-07T16:46:06.439Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on real H*-algebras

Published online by Cambridge University Press:  24 October 2008

M. Cabrera ,
J. Martinez  and
A. Rodriguez
M. Cabrera
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071-Granada, Spain
J. Martinez
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071-Granada, Spain
A. Rodriguez
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071-Granada, Spain
Get access Rights & Permissions [Opens in a new window]

Extract

Complex (associative) H*-algebras were introduced and studied in detail by Ambrose[1]; it was proved that every complex H*-algebra with zero annihilator is the l2-sum of a suitable family of topologically simple complex H*-algebras and that the H*-algebras 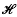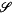(H) of all Hilbert-Schmidt operators on any complex Hilbert space H are the only topologically simple complex H*-algebras. In a recent paper [2] Balachandran and Swaminathan observe that the reduction of the theory of real H*-algebras to the topologically simple case follows easily with minor changes of the complex argument, and they prove a theorem describing topologically simple real H*-algebras. This theorem can be equivalently reformulated as follows.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 131 - 132
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambrose, W.. Structure theorems for a special class of Banach algebras. Trans. Amer. Math. Soc. 57 (1945), 364–386.CrossRefGoogle Scholar
[2]Balachandran, V. K. and Swaminathan, N.. Real H*-algebras. J. Funct. Anal. 65 (1986), 64–75.CrossRefGoogle Scholar
[3]Hanche-Olsen, H. and St⊘rmer, E.. Jordan Operator Algebras (Pitman, 1984).Google Scholar
[4]Rickart, C. E.. General Theory of Banach Algebras (Van Nostrand, 1960).Google Scholar