Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T12:56:23.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-trivial links and plats with trivial Gassner matrices

Published online by Cambridge University Press:  24 October 2008

Tim D. Cochran
Tim D. Cochran
Affiliation:
Mathematics Department, Rice university, P.O. Box 1892, Houston, Texas 77251-1892, USA
Get access Rights & Permissions [Opens in a new window]

Extract

Let Bn denote the Artin braid group on ‘n-strings[ and PBn its normal subgroup consisting of all the pure braids [Bi, Mo]. These groups have been considerably scrutinized by both topologists and algebraists [BL]. One question whose answer has so far eluded us is whether or not the Gassner representation G: PBn → Mn × n(λ), into the group of n-by-n matrices over 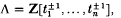, is faithful (see Section 1) [Bi; ·3] [Ga]. Recently the less discriminating Burau representation B: PBn → Mn × n(Z[t±1] ) was shown to have a non-trivial kernel for each n ≥ 6 [M, LP] but these techniques have not yet yielded an element of kernel(G). This paper is a partial step in that direction.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 1 , January 1996 , pp. 43 - 53
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BX]Bar-Natan, D.. Vassiliev homotopy string link invariants, preprint, Harvard University, 1993.Google Scholar
[Bi]Birman, Joan S.. Braids, Links and Mapping Class Groups, Annals of Math. Studies 82 (Princeton University Press 1975).Google Scholar
[BLBirman, J. S. and Libgober, A. eds. Braids: Proceedings of a Summer Research Conference held July 13–26, 1986, Contemperary Mathematics volume 78 (American Mathematical Society, 1988).Google Scholar
[C1]Cochran, Tim D.. Links with trivial Alexander's Module but non-vanishing Massey Products, Topology 29 (1990), 189–204.Google Scholar
[C2]Cochran, Tim D.. Derivatives of Links: Milnor's invariants and Massey products, Memoirs of Amer. Math. Soc. 427, Vol. 84 (American Mathematical Society, 1990).Google Scholar
[CL]Cooper, D. and Long, D. D.. Derivative varieties and the pure braid group. American Journal of Math. 115 (1993), 137–160.CrossRefGoogle Scholar
[Cr]Crowell, R. H.. The derived module of a homomorphism. Adv. in Math. 6 (1971), 210–238.Google Scholar
[F]Fox, R. H.. Quick trip through knot theory, topology of 3-manifolds and related topics (Fort, M. K., ed.) (Prentice Hall, 1962).Google Scholar
[Ga]Gassner, . On braid groups. Abh. Math. Sem. Hamburg Univ. 25 (1961), 19–22.CrossRefGoogle Scholar
[G]Goldsmith, D. L.. Homotopy of braids: in answer to a question of Artin, Topology Conference VPI 1973, Lecture Notes in Mathematics 375 (Springer Verlag, 1974).Google Scholar
[HL]Habegger, N. and Xiao-Song, Lin. The classification of links up to link-homotopy. J. Amer. Math. Soc. 3 (1990), 389–419.CrossRefGoogle Scholar
[H1]Hillman, J. A.. A link with Alexander module free which is not an homology boundary link. J. Pure Appl Alg. 20 (1981), 1–5.CrossRefGoogle Scholar
[H2]Hillman, J. A.. Alexander Ideals of Links, Lecture Notes in Math. 895 (Springer-Verlag, 1981).CrossRefGoogle Scholar
[La]Lambert, H. W.. A 1-linked link whose longitudes lie in the second commutator subgroup. Trans. Amer. Math. Soc. 147 (1970), 261–269.CrossRefGoogle Scholar
[Li]Lin, Xiao-Song. Artin-type representation theorems and Milnor's μ¯-invariants. Ph.D. thesis, University of California at San Diego, 1988.Google Scholar
[Li2]Lin, Xiao-Song. Milnor link invariants are all of finite type, preprint, Columbia University, 1993.Google Scholar
[Mi1]Milnor, J.. Link groups. Annals of Math. 59 (1954), 177–195.CrossRefGoogle Scholar
[Mi2]Milnor, J.. Isotopy of links, Algebraic geometry and topology: A symposium in honor of S. Lefshetz, (Princeton University Press, 1957), 280–306.CrossRefGoogle Scholar
[M]Moody, J.. The Burau representation is unfaithful for large n. Bull. Amer. Math. Soc. 25 (1991), 379–384.CrossRefGoogle Scholar
[Mo]Moran, Siegfried. The mathematical theory of knots and braids: an introduction. North Holland Mathematics Studies 82 (Elsevier Science Publishers E.V., 1983).Google Scholar
[Po]Porter, Richard. Milnor's μ¯-invariants and Massey products. Trans. Amer. Math. Soc. 257 (1980), 39–71.Google Scholar
[Sm]Mythe, N. S.. Isotopy invariants of links and the Alexander matrix. Amer. Journal of Math. 89 (1967), 693–704.Google Scholar
[St]Stanford, T.. Braid commutators and finite type invariants of knots and links, preprint, University of Geneva, 1993.Google Scholar
[Tr]Traldi, Lorenzo. Milnor's invariants and the completions of link modules. Trans. Amer. Math. Soc. 284 (1984), 401–423.Google Scholar
[Tu]Turaev, V. G.. The Milnor invariants and Massey products. In Studies in Topology-II, Zap. Nanc. Sem. Lenin. Ot. Mat. Kogo oi Stet. Acad. Nauk USSR 66 (1976)Google Scholar
Turaev, V. G.. in translation Journal of Soviet Mathematics 12 (1979), no. 1.Google Scholar