Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Adams, Colin
Hoste, Jim
and
Palmer, Martin
2019.
Triple-crossing number and moves on triple-crossing link diagrams.
Journal of Knot Theory and Its Ramifications,
Vol. 28,
Issue. 11,
p.
1940001.
Jabłonowski, Michał
and
Trojanowski, Łukasz
2020.
Triple-crossing projections, moves on knots and links and their minimal diagrams.
Journal of Knot Theory and Its Ramifications,
Vol. 29,
Issue. 04,
p.
2050015.
Jabłonowski, Michał
2020.
Triple-crossing number, the genus of a knot or link and torus knots.
Topology and its Applications,
Vol. 285,
Issue. ,
p.
107389.
Guha, Anshul
2022.
A new bound on odd multicrossing numbers of knots and links.
Journal of Knot Theory and Its Ramifications,
Vol. 31,
Issue. 02,
Hagedorn, Nicholas D.
2023.
Strict inequalities for the n-crossing number.
Journal of Knot Theory and Its Ramifications,
Vol. 32,
Issue. 04,
Adams, Colin
Even-Zohar, Chaim
Greenberg, Jonah
Kaufman, Reuben
Lee, David
Li, Darin
Ping, Dustin
Sandstrom, Theodore
and
Wang, Xiwen
2023.
Virtual multicrossings and petal diagrams for virtual knots and links.
Journal of Knot Theory and Its Ramifications,
Vol. 32,
Issue. 08,
JABŁONOWSKI, Michał
2023.
Tabulation of Knots Up to Five Triple-crossings and Moves between Oriented Diagrams.
Tokyo Journal of Mathematics,
Vol. 46,
Issue. 1,
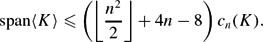 $$\text{span} \langle K \rangle \leq \left(\left\lfloor\frac{n^2}{2}\right\rfloor + 4n - 8\right) c_n(K).$$
$$\text{span} \langle K \rangle \leq \left(\left\lfloor\frac{n^2}{2}\right\rfloor + 4n - 8\right) c_n(K).$$