Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T14:30:17.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix summability of Fourier series based on inclusion theorems

Published online by Cambridge University Press:  24 October 2008

B. E. Rhoades
B. E. Rhoades
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let 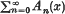denote the Fourier series expansion of a function 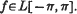. Féver's celebrated theorem states that the series is summable (C, 1) at each point of continuity of f, where (C, 1) denotes the Cesàro method of summability of order 1. Riesz extended this result to (C, α) for each α > 0. Since then many authors have established sufficient conditions on various methods of summability to guarantee similar results. Over the years the pattern has been to strive for weaker conditions on the matrix, and to replace the condition of continuity on the function by a less stringent one. Theorems have been proved not only for the summability of f, but the summability of the derived series, and other series, related to f. Beginning with the work of Hille and Tamarkin[13], many of the theorems have been extended to absolute summability.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 3 , November 1986 , pp. 545 - 557
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Astrachan, M.. Studies in the summability of Fourier series by Nörlund means. Duke Math J. 2 (1936), 543–568.CrossRefGoogle Scholar
[2]Bosanquet, L. S.. On the summability of Fourier series. Proc. London Math. Soc. 31 (1930), 144–160.CrossRefGoogle Scholar
[3]Chow, H. C.. On a theorem of O. Szasz. J. London Math. Soc. 16 (1941), 23–27.CrossRefGoogle Scholar
[4]Das, G. and Mohapatra, P. C.. Necessary and sufficient conditions for absolute Nörlund summability of Fourier series. Proc. London Math. Soc. 41 (1980), 217–253.CrossRefGoogle Scholar
[5]Dikshit, H. P.. The Nörlund summability of the conjugate series of a Fourier series. Rend. Circ. Mat. Palermo 11 (1962), 217–224.CrossRefGoogle Scholar
[6]Dikshit, H. P.. On the Nörlund summability of the conjugate series of Fourier series. Rend. Circ. Mat. Palermo 14 (1965), 165–170.CrossRefGoogle Scholar
[7]Dikshit, H. P.. Summability of Fourier series by triangular matrix transformations. Pacific J. Math. 30 (1969), 399–410.CrossRefGoogle Scholar
[8]Dikshit, H. P.. Summability of a sequence of Fourier coefficients by a triangular matrix transformation. Proc. Amer. Math. Soc. 21 (1969), 10–20.CrossRefGoogle Scholar
[9]Dikshit, H. P.. Absolute total-effective triangular matrix method. Math. Ann. 186 (1970), 101–113.CrossRefGoogle Scholar
[10]Dikshit, H. P.. Absolute total-effective (N, pn) means. Proc. Cambridge Philos. Soc. 69 (1971), 107–122.CrossRefGoogle Scholar
[11]Dikshit, H. P. and Kumar, A.. Determination of bounds similar to the Lebesgue constants. Pacific J. Math. 97 (1981), 339–347.CrossRefGoogle Scholar
[12]Fejer, L.. Uber die Bestimmung des Sprunges der Funktion aus ihrer Fourierreihe. J. Reine Angew. Math. 142 (1913), 165–188.CrossRefGoogle Scholar
[13]Hardy, G. H.. Divergent Series (Oxford University Press, 1949).Google Scholar
[14]Hille, E. and Tamarkin, J. D.. On the summability of Fourier series, I. Trans. Amer. Math. Soc. 34 (1932), 757–783.CrossRefGoogle Scholar
[15]Hsiang, G. C.. Summability (L) of Fourier series. Bull. Amer. Math. Soc. 67 (1961), 150–153.CrossRefGoogle Scholar
[16]Iyengar, K. S. K.. A Tauberian theorem and its application to convergence of Fourier series. Proc. Indian Acad. Sci. (A) 18 (1943), 81–87.CrossRefGoogle Scholar
[17]Karamata, J.. Remarque relative à la sommation des series de Fourier par le procédé de Nörlund. Publ. Sci, L'Univ. d'Alger. 1 (1954), 7–13.Google Scholar
[18]Knopp, K.. Theory and Application of Infinite Series. (Blackie and Sons, 1947.)Google Scholar
[19]Kumar, A.. Absolute total-effectiveness of a total effective (N, pn) method. Proc. Amer. Math. Soc. 84 (1982), 497–503.Google Scholar
[20]Paley, R. E. A. C.. On the Cesàro summability of Fourier series and allied series. Proc. Cambridge Philos. Soc. 26 (1930), 173–203.CrossRefGoogle Scholar
[21]Prasad, B. N. and Siddiqi, J.. On the Nörlund summability of derived Fourier series. Proc. Nat. Inst. Sci. India 16 (1950), 71–82.Google Scholar
[22]Rhoades, B. E.. Matrix summability of Fourier series based on inclusion theorems, II (to appear).Google Scholar
[23]Siddiqi, J. A.. The determination of the jump of a function by Nörlund means. Publ. Math. Debrecen 25 (1978), 5–19.CrossRefGoogle Scholar
[24]Silverman, L. L.. Products of Nörlund transformations. Bull. Amer. Math. Soc. 43 (1937), 95–101.CrossRefGoogle Scholar
[25]Singh, T.. Absolute Nörlund summability of Fourier series. Indian J. Math. 6 (1964), 129–136.Google Scholar
[26]Singh, T.. Nörlund summability of Fourier series and its conjugate series. Ann. Mat. Pura Appl. 64 (1964), 123–132.CrossRefGoogle Scholar
[27]Thorpe, B.. Nörlund summability of Jacobi and Laguerre series. J. reine angew. Math. 276 (1975), 137–141.Google Scholar
[28]Zygmund, A.. Trigonometric Series, vol. I (Cambridge University Press, 2nd ed. 1959).Google Scholar
[29]Das, G.. Product of Nörlund methods. Indian J. Math. 10 (1968), 25–43.Google Scholar