Article contents
Matchings and Radon transforms in lattices II. Concordant sets
Published online by Cambridge University Press: 24 October 2008
Abstract
Let 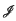 and ℳ be subsets of a finite lattice L.
and ℳ be subsets of a finite lattice L. 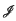 is said to be concordant with ℳ if, for every element x in L, either x is in ℳ or there exists an element x+ such that (CS1) the Möbius function μ(x, x+) ≠ 0 and (CS2) for every element j in
is said to be concordant with ℳ if, for every element x in L, either x is in ℳ or there exists an element x+ such that (CS1) the Möbius function μ(x, x+) ≠ 0 and (CS2) for every element j in 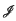 , x ∨ j ≠ x+. We prove that if
, x ∨ j ≠ x+. We prove that if 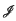 is concordant with ℳ, then the incidence matrix I(ℳ |
is concordant with ℳ, then the incidence matrix I(ℳ | 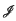 ) has maximum possible rank |
) has maximum possible rank |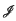 |, and hence there exists an injection σ:
|, and hence there exists an injection σ: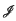 → ℳ such that σ(j) ≥ j for all j in
→ ℳ such that σ(j) ≥ j for all j in 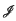 . Using this, we derive several rank and covering inequalities in finite lattices. Among the results are generalizations of the Dowling-Wilson inequalities and Dilworth's covering theorem to semimodular lattices, and a refinement of Dilworth's covering theorem for modular lattices.
. Using this, we derive several rank and covering inequalities in finite lattices. Among the results are generalizations of the Dowling-Wilson inequalities and Dilworth's covering theorem to semimodular lattices, and a refinement of Dilworth's covering theorem for modular lattices.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 2 , March 1987 , pp. 221 - 231
- Copyright
- Copyright © Cambridge Philosophical Society 1987
References
REFERENCES
- 6
- Cited by


