Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T00:40:17.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometries of self-adjoint complex function spaces

Published online by Cambridge University Press:  24 October 2008

A. J. Ellis
A. J. Ellis
Affiliation:
Department of Mathematics, University of Hong Kong, Hong Kong
Get access Rights & Permissions [Opens in a new window]

Extract

By a complex function space A we will mean a uniformly closed linear space of continuous complex-valued functions on a compact Hausdorff space X, such that A contains constants and separates the points of X. We denote by S the state-space

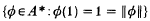
endowed with the w*-topology. If A is self-adjoint then it is well known (cf. [1]) that A is naturally isometrically isomorphic to 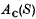, and re A is naturally isometrically isomorphic to A(S), where 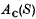(respectively A(S)) denotes the Banach space of all complex-valued (respectively real-valued) continuous affine functions on S with the supremum norm.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 133 - 138
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Asimow, L. and Ellis, A. J.. Convexity Theory and its Applications in Functional Analysis. London Math. Soc. Monographs no. 16 (Academic Press, 1980).Google Scholar
[2]Ellis, A. J.. Equivalence for complex state spaces of function spaces. Bull. London Math. Soc. 19 (1987), 359–362.CrossRefGoogle Scholar
[3]Ellis, A. J. and So, W. S.. Isometries and the complex state spaces of uniform algebras. Math. Z. 195 (1987), 119–125.CrossRefGoogle Scholar
[4]Lazar, A. J.. Affine products of simplexes. Math. Scand. 22 (1968), 165–175.CrossRefGoogle Scholar
[5]Rao, T. S. S. R. K.. Isometries of A c(K). Proc. Amer. Math. Soc. 85 (1982), 544–546.Google Scholar