Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zalesskiĭ, A. E.
1995.
Finite and Locally Finite Groups.
p.
219.
Leinen, Felix
and
Puglisi, Orazio
2002.
Confined subgroups in periodic simple finitary linear groups.
Israel Journal of Mathematics,
Vol. 128,
Issue. 1,
p.
285.
Leinen, Felix
and
Puglisi, Orazio
2002.
Ideals in group algebras of simple locally finite groups of 1-type.
Pacific Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
433.
Leinen, Felix
and
Puglisi, Orazio
2005.
Some results concerning simple locally finite groups of 1-type.
Journal of Algebra,
Vol. 287,
Issue. 1,
p.
32.
Leinen, Felix
and
Puglisi, Orazio
2007.
Positive definite functions of finitary isometry groups over fields of odd characteristic.
Journal of Pure and Applied Algebra,
Vol. 208,
Issue. 3,
p.
1003.


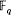 be the field with
be the field with