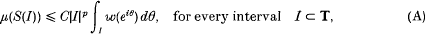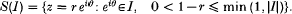Research Article
On sums of two squarefull numbers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
-
- Article
- Export citation
The ideal lattices of the complex group rings of finitary special and general linear groups over finite fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 7-25
-
- Article
- Export citation
Permissible symmetries of coupled cell networks
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-36
-
- Article
- Export citation
On Schur algebras and related algebras III: integral representations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-55
-
- Article
- Export citation
Diophantine approximation in Kleinian groups†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-78
-
- Article
- Export citation
Locally compact groups whose conjugation representations satisfy a Kazhdan type property or have countable support
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-97
-
- Article
- Export citation
Subsemigroups of Stone-Čech compactifications
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-118
-
- Article
- Export citation
Triple points of unknotting discs and the Arf invariant of knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-129
-
- Article
- Export citation
The even master system and generalized Kummer surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-142
-
- Article
- Export citation
Convolution estimates for some degenerate curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 143-146
-
- Article
- Export citation
The L2-
 -problem on manifolds with piecewise strictly pseudoconvex boundaries
-problem on manifolds with piecewise strictly pseudoconvex boundaries
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-149
-
- Article
- Export citation
Embedding derivatives of weighted Hardy spaces into Lebesgue spaces1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 151-166
-
- Article
- Export citation
On the Friedrichs extension of semi-bounded difference operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-177
-
- Article
- Export citation
Renewal theory in a random environment
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-190
-
- Article
- Export citation
Corrigendum
Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 191
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 116 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 116 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation


 be the field with
be the field with 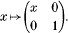
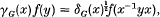
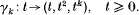
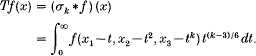
 -problem on manifolds with piecewise strictly pseudoconvex boundaries
-problem on manifolds with piecewise strictly pseudoconvex boundaries