Graphs in the plane invariant under an area preserving linear map and general continuous solutions of certain quadratic functional equations

Abstract

The requirement that the graph 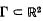of a function be invariant under a linear map 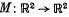is equivalent to a functional equation of f. For area preserving maps M(det (M) = 1), the functional equation is equivalent to an (easily solved) linear one, or to a quadratic one of the form

for all Here 2C = Trace (M). It is shown that (Q) admits continuous solutions ⇔ M has real eigenvalues ⇔ (Q) has linear solutions f(x) = λx ⇔ |C| ≥ 1. For |c| = 1 or C < – 1, (Q) only admits a few simple solutions. For C > 1, (Q) admits a rich supply of continuous solutions. These are parametrised by an arbitrary function, and described in the sense that a construction is given for the graphs of the functions which solve (Q).