Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T01:22:31.351Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometrical aspects of the theory of non-homogeneous Markov chains

Published online by Cambridge University Press:  24 October 2008

J. F. C. Kingman
J. F. C. Kingman
Affiliation:
Mathematical Institute, University of Oxford
Get access Rights & Permissions [Opens in a new window]

Abstract

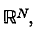A geometrical representation of the transition matrices of a non-homogeneous chain with N states, in terms of certain convex subsets of , is used to describe aspects of the chain. For example, an important theorem of Cohn on the structure of the tail σ-field is a simple corollary. The embedding problem is shown to be entirely geometrical in character. The representation extends to Markov processes on quite general state spaces, and the tail is then represented by the projective limit of these convex sets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 171 - 183
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cohn, H.On the tail σ-algebra of the finite inhomogeneous Markov chains. Ann. Math. Statist. 41 (1970), 2175–2176.CrossRefGoogle Scholar
(2)Cohn, H.On the tail events of a Markov chain. Z. Wahrscheinlichkeitstheorie 29 (1974), 65–72.CrossRefGoogle Scholar
(3)Dobrusin, R. L.Central limit theorem for nonstationary Markov chains I. Theory Prob. Appl. 1 (1956), 65–80.CrossRefGoogle Scholar
(4)Dobrusin, R. L.Central limit theorem for nonstationary Markov chains II. Theory Prob. Appl. 1 (1956), 329–383.CrossRefGoogle Scholar
(5)Goodman, G. S.An intrinsic time for non-stationary finite Markov chains. Z. Wahrscheinlichkeitstheorie 16 (1970), 165–180.CrossRefGoogle Scholar
(6)Goodman, G. S. and Johansen, S.Kolrnogorov's differential equations for non-stationary, countable state space Markov processes with uniformly continuous transition probabilities. Proc. Camb. Phil. Soc. 73 (1973), 119–138.CrossRefGoogle Scholar
(7)Iosifescu, M.On finite tail σ-algebras. Z. Wahrscheinlichkeitstheorie 24 (1972), 159–166.CrossRefGoogle Scholar
(8)Iosifescu, M.On two recent papers on ergodicity in non-homogeneous Markov chains. Ann. Math. Statist. 43 (1972), 1732–1736.CrossRefGoogle Scholar
(9)Iosifesou, M. and Theodorescu, R.Random processes and learning (Springer, 1969).CrossRefGoogle Scholar
(10)Jacobsen, M.Characterization of minimal Markov jump processes. Z. Wahrscheinlichkeitstheorie 23 (1972), 32–46.CrossRefGoogle Scholar
(11)Johansen, S.The bang–bang problem for stochastic matrices. Z. Wahrscheinlichkeitstheorie 26 (1973), 191–195.CrossRefGoogle Scholar
(12)Kendall, D. G. An introduction to stochastic analysis, published in Stochastic analysas (ed. Kendall, D. C. and Harding, E. F., Wiley, 1973).Google Scholar
(13)Kingman, J. F. C. and Williams, D.The combinatorial structure of non-homogeneous Markov chains. Z. Wahrscheinlichkeitstheorie 26 (1973), 77–86.CrossRefGoogle Scholar
(14)Seneta, E.On the historical development of the theory of inhomogeneous Markov chains. Proc. Camb. Phil. Soc. 74 (1973), 507–513.CrossRefGoogle Scholar