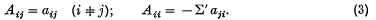Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T12:20:39.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence of two absorption problems with Markovian transitions and continuous or discrete time parameters

Published online by Cambridge University Press:  24 October 2008

R. A. Sack
R. A. Sack
Affiliation:
Department of Theoretical ChemistryUniversity of Cambridge British Rayon Research AssociationWythenshawe Manchester†
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. Ledermann(1) has treated the problem of calculating the asymptotic probabilities that a system will be found in any one of a finite number N of possible states if transitions between these states occur as Markov processes with a continuous time parameter t. If we denote by pi(t) the probability that at time t the system is in the ith state and by aij ( ≥ 0) the constant probability per unit time for transitions from the jth to the ith state, the rate of change of pi is given by

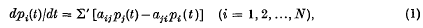
where the sum is to be taken over all j ≠ i. This set of equations can be written in matrix form as

where P(t) is the vector with components pi(t) and the constant matrix A has elements

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 55 , Issue 2 , April 1959 , pp. 177 - 180
Copyright
Copyright © Cambridge Philosophical Society 1959

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ledermann, W.On the asymptotic distribution for certain Markoff processes. Proc. Camb. Phil. Soc. 46 (1950), 581–94; and 47 (1951), 626.CrossRefGoogle Scholar
(2)Feller, W.An introduction to probability theory and its applications, Vol. I, Chapters 15, 16. (New York, 1951.)Google Scholar
(3)Goddard, L. S.Transition matrices occurring in the theory of Markoff processes. Proc. Camb. Phil. Soc. 51 (1955), 382–4.CrossRefGoogle Scholar
(4)Giovanelli, R. G.The hydrogen spectrum of the sun. Mon. Not. R. Astr. Soc. 109 (1949), 298.CrossRefGoogle Scholar
(5)Giovanelli, R. G. and Jefferies, J. T.The albedo for the atomic scattering of optical radiation. Austr. J. Phys. 7 (1954), 570–4.CrossRefGoogle Scholar