Countable lattice-ordered groups

Extract

A lattice-ordered group is a group and a lattice such that the group operation distributes through the lattice operations (i.e. f(g ∨ h)k = fgk ∨ fhk and dually). Lattice-ordered groups are torsion-free groups and distributive lattices. They further satisfy f ∧ g = (f⁻¹ ∨ g⁻¹)⁻¹ and f ∨ g = (f⁻¹ ∧ g⁻¹)⁻¹. Since the lattice is distributive, each lattice-ordered group word can be written in the form ∨_A ∧_B ω_αβ where A and B are finite and each ω_αβ is a group word in {x_i: i ∈ I}. Unfortunately, even for free lattice-ordered groups, this form is not unique. We will use the prefix l- for maps between lattice-ordered groups that preserve both the group and lattice operations, and e for the identity element. A presentation (x_i;r_j(x) = e)_i∈I, _j∈J is the quotient of the free lattice-ordered group F on {x_i: i∈I} by the l-ideal (convex normal sublattice subgroup) generated by its subset {r_j(x): j ∈ J}. {x_i: i ∈ I} is called a generating set and {r_i(x):j∈J} a defining set of relations. If I and J are finite we have a finitely presented lattice-ordered group. If 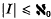we can effectively enumerate all lattice-ordered group words r₁(x), r₂(x),… in x_i; i∈I}. If I is finite and J (for this enumeration) is a recursively enumerable set, we say that we have a recursively presented lattice-ordered group. Throughout Z denotes the group of integers and ℝ the real line.

Our purpose in this paper is to prove the natural analogues of three theorems from combinatorial group theory (5), chapter IV, theorems 4·9, 3·1 and 3·5-in particular, theorem C is a natural analogue of an unpublished theorem of Philip Hall (4).