Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T03:15:11.181Z Has data issue: false hasContentIssue false
  • English
  • Français

The convolution metric dg

Published online by Cambridge University Press:  24 October 2008

J. E. Yukich
J. E. Yukich
Affiliation:
Université Louis Pasteur, Strasbourg, France
Get access Rights & Permissions [Opens in a new window]

Abstract

Summary

We introduce and study a new metric on 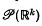denned by

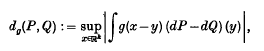
where 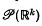is the space of probability measures on ℝk and where g: ℝk→ is a probability density satisfying certain mild conditions. The metric dg, relatively easy to compute, is shown to have useful and interesting properties not enjoyed by some other metrics on 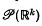. In particular, letting pn denote the nth empirical measure for P, it is shown that under appropriate conditions 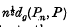satisfies a compact law of the iterated logarithm, converges in probability to the supremum of a Gaussian process, and has a useful stochastic integral representation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 3 , November 1985 , pp. 533 - 540
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Billingsley, P.. Convergence of Probability Measures. (Wiley, 1968).Google Scholar
[2]Dudley, R. M.. Convergence of Baire measures. Studio Math. 27 (1966), 251–268.CrossRefGoogle Scholar
[3]Dudley, R. M.. The speed of mean Glivenko-Cantelli convergence. Annals of Math. Stat. (1) 40 (1969), 40–50.CrossRefGoogle Scholar
[4]Dudley, R. M.. Central limit theorems for empirical measures. Ann. Probab. 6 (1978), 899–929, correction, 7 (1979), 909–911.CrossRefGoogle Scholar
[5]Dudley, R. M.. Donsker classes of functions. Statistics and Related Topics (Proc. Symp. Ottawa, 1980) (North Holland, 1981), 341–352.Google Scholar
[6]Dudley, R. M.. A Course on Empirical Processes. Lecture Notes in Mathematics, no. 1097 (Springer-Verlag, 1984).Google Scholar
[7]Dudley, R. M. and Philipp, W.. Invariance principles for sums of Banach space valued random elements and empirical processes. Z. Wahrschein. 62 (1983), 509–552.CrossRefGoogle Scholar
[8]Feller, W.. An Introduction to Probability Theory and Its Applications (Wiley, 1968).Google Scholar
[9]Fortet, R. and Mourier, E.. Convergence de la répartition empirique vers la répartition théorique. Ann. Sci. Ecole Norm. Sup. 70 (1953), 266–285.Google Scholar
[10]Jain, N. C. and Marcus, M. B.. Central limit theorems for C(S) valued random variables. J. Funct. Anal. 19 (1975), 216–231.CrossRefGoogle Scholar
[11]Kuelbs, J. and Dudley, R. M.. Log log laws for empirical measures. Ann. Probab. 8 (1980), 405–418.CrossRefGoogle Scholar
[12]Rudin, W.. Fourier Analysis on Groups (Interscience Publishers, 1962).Google Scholar
[13]Zolotarev, V. M.. Probability metrics. Theory Probab. Appl. 28 (2) (1984), 278–302.CrossRefGoogle Scholar
[14]Zuker, M.. Speeds of convergence of random probability measures. Ph.D. Dissertation, M.I.T. (1974).Google Scholar