Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:19:31.598Z Has data issue: false hasContentIssue false
  • English
  • Français

The convergence of polynomial expansions of positive harmonic functions

Published online by Cambridge University Press:  24 October 2008

D. H. Armitage
D. H. Armitage
Affiliation:
Department of Pure Mathematics, Queen's University, Belfast BT7 1NN
Get access Rights & Permissions [Opens in a new window]

Extract

Let B(r) denote the open ball of radius r centred at the origin 0 of the Euclidean space ℝN, where N ≥ 2. It is well known that if h is harmonic in B(1), then there exist homogeneous harmonic polynomials Hj of degree j in ℝN such that 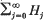converges absolutely and locally uniformly to h in B(1) (see, e.g. Brelot[1], Appendice). Further, this series is unique and each Hj is the sum of all the monomial terms of degree j in the multiple Taylor series of h centred at 0. We call 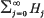the polynomial expansion of h.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 1 , January 1995 , pp. 165 - 174
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Brelot, M.. Éléments de la théorie classique du potentiel (Centre de documentation universitaire, Paris, 1969).Google Scholar
[2]Doob, J. L.. Classical Potential Theory and Its Probabilistic Counterpart (Springer, 1983).Google Scholar
[3]Fejér, L.. Über die Laplacesche Reihe. Math. Ann. 67 (1909), 76–109.CrossRefGoogle Scholar
[4]Fejér, L., Über die Positivität von Summen, die nach trigonometrischen oder Legendreschen Funktionen fortschreiten (Erste Mitteilung), Acta litterarum ac scientiarum regiae universitatis hungaricae Francisco-Josephinae. secto scientiarum mathematicarum 2 (1925), 75–86.Google Scholar
[5]Feldheim, E.. On the positivity of certain sums of ultraspherical polynomials. J. d'Analyse Math. 11 (1963), 275–284.CrossRefGoogle Scholar
[6]Müller, C.. Spherical Harmonics (Lecture Notes in Math, vol. 17, Springer, 1966).CrossRefGoogle Scholar
[7]Szegö, G.. Koeffizientenabschätzungen bei ebenen und räumlichen harmonischen Ent-wicklungen. Math. Ann. 96 (1927), 601–632.CrossRefGoogle Scholar
[8]Szegö, G.. Orthogonal Polynomials (American Mathematical Society, 1967).Google Scholar