Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:01:17.384Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic analysis of the Cooke-Noble integral equation

Published online by Cambridge University Press:  24 October 2008

L. R. F. Rose
L. R. F. Rose
Affiliation:
Aeronautical Research Laboratories, Melbourne 3207, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

Those mixed boundary-value problems which can usefully be treated analytically often lead to the following mathematical problem. Two functions u(x), σ(x), defined over the interval ([0, ∞), take prescribed values over complementary portions of that interval; specifically, let

where p(x) is usually a simple function, for example a constant or a power of x. There exists a relation between u(x) and σ(x) which can be most simply expressed as a relation between their Hankel transforms. Using a circumflex to denote the Hankel transform, for example with

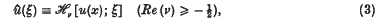
where Jv denotes as usual the Bessel function of the first kind of order v, we can state that relation between u and σ as follows:

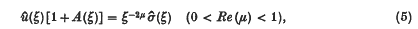
where A(ξ) is a known function, determined at an earlier stage of the analysis. The problem is to derive u(x) for (xє [ 0, a), or σ(x) for x є (a, ∞).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 2 , September 1982 , pp. 293 - 306
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Abramowitz, M. and Stegun, I. A.Handbook of mathematical functions (Dover, 1965) p. 487, no. 11.4.41.Google Scholar
(2)Anderssen, R. S., De Hoog, F. R. and Rose, L. R. F.Explicit solutions for a class of dual integral equations. Proc. Roy. Soc. Edin. (in press, 1982).Google Scholar
(3)Bleistein, N. and Handelsman, R. A.Asymptotic expansions of integrals, chap. 4 (Holt, Rinehart and Winston, 1975).Google Scholar
(4)Cooke, J. C.A solution of Tranter's dual integral equations problem. Quart. J. Mech. App. Math. 9 (1956), 103–110.Google Scholar
(5)Davies, B.Integral transforms and their applications, §§ 12, 14 (Springer-Verlag, 1978).CrossRefGoogle Scholar
(6)England, A. H. and Green, A. E.Some two-dimensional punch and crack problems in classical elasticity. Proc. Cambridge Phil. Soc. 59 (1963), 489–500.CrossRefGoogle Scholar
(7)Erdelyi, A. (ed.). Higher transcendental functions, vol. 1, p. 68 (McGraw-Hill, 1953).Google Scholar
(8)Jones, D. S.Diffraction at high frequencies by a circular disc. Proc. Cambridge Phil. Soc. 61 (1965), 223–245.CrossRefGoogle Scholar
(9)Handelsman, R. A. and Lew, J. S.Asymptotic expansion of a class of integral transforms with algebraically dominated kernels. J. Math. Anal. Applies. 35 (1971), 405–433.CrossRefGoogle Scholar
(10)Noble, B.Certain dual integral equations. J. Math. Phys. 37 (1958), 128–136.Google Scholar
(11)Noble, B.The solution of Bessel function dual integral equations by a multiplying-factor method. Proc. Cambridge Phil. Soc. 59 (1963), 351–362.Google Scholar
(12)Rose, L. R. F.A cracked plate repaired by bounded reinforcements. Int. J. Fracture 18 (1982), 135–144.Google Scholar
(13)Sneddon, I. N.Mixed boundary valve problems in potential theory, chap. 4 (North Holland, 1966).Google Scholar
(14)Sneddon, I. N. and Lowengrub, M.Crack problems in the classical theory of elasticity (Wiley, 1969).Google Scholar
(15)Watson, G. N.A treatise on the theory of Bessel functions (Cambridge, 1944).Google Scholar
(16)Zabreyko, P. P. et al. Integral equations: a reference text, chap. 2, §6 (Noordhoff, 1975).Google Scholar