Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T17:09:51.533Z Has data issue: false hasContentIssue false
  • English
  • Français

An integral which occurs in statistics

Published online by Cambridge University Press:  24 October 2008

A. E. Ingham
A. E. Ingham
Affiliation:
King's College
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this note we give a direct evaluation of the integral

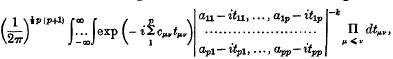
whose value has been inferred from the theory of statistics. Here A = Ap = (αμν) and C = Cp = (Cμν) are real symmetrical matrices, of which A is positive definite; there are ½ p (p + 1) independent variables of integration tμν (1 ≤ μ ≤ ν ≤ p), and tμν is written also as tνμ for symmetry of notation; in the summation ∑ the variables μ, ν run independently from 1 to p; k is a real number. A word of explanation is necessary with regard to the determination of the power |A − iT|−k. Since A is positive definite and T real and symmetric, the roots of the equation

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 2 , May 1933 , pp. 271 - 276
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Wishart, J., Biometrika, 20 A (1928), 32–52CrossRefGoogle Scholar; Wishart, J. and Bartlett, M. S., Proc. Camb. Philos. Soc. 29 (1933), 260–270CrossRefGoogle Scholar (the paper preceding this).

† We denote a square matrix (αμν) of p rows and columns by A p or A, and its determinant by |A| or |A p|; with a similar notation in other letters. A real symmetric matrix A is ‘positive definite’ if the associated quadratic form is positive definite; by this we mean that A (x, x) > 0 for all real values of x 1, …, x p not all 0 (i.e. we use ‘positive definite’ in the sense of ‘positive and non-singular’ or ‘positive and of rank p’).

To avoid confusion with the notation |A| we denote the modulus of a complex number z by |z|, and the modulus of |A| by |A|.

* Cf. Wishart and Bartlett, loc. cit., 261. To reduce our integral to their form (c) we take the integrals along the imaginary axes (as we may by Cauchy's theorem) and write υμ = iu μ, noting that