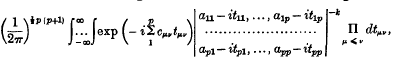Research Article
An extension of Morley's chain of theorems on circles*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-172
-
- Article
- Export citation
On the product of two Legendre polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-177
-
- Article
- Export citation
Some surfaces containing triple curves, II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-183
-
- Article
- Export citation
On surfaces of sectional genus four
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 184-194
-
- Article
- Export citation
Related quadrics and systems of a rational quartic curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-206
-
- Article
- Export citation
The general double integral problem in the calculus of variations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-211
-
- Article
- Export citation
Isolated singular points in the theory of algebraic surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-230
-
- Article
- Export citation
On Gauss's proof of the normal law of errors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-234
-
- Article
- Export citation
Incidence scrolls
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 235-244
-
- Article
- Export citation
The sums of powers as simultaneous canonical expressions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-256
-
- Article
- Export citation
A theorem on transitive groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-259
-
- Article
- Export citation
The generalised product moment distribution in a normal system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-270
-
- Article
- Export citation
An integral which occurs in statistics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-276
-
- Article
- Export citation
Slow rotation of a circular cylinder in a viscous fluid bounded by parallel walls
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-287
-
- Article
- Export citation
The effect of a magnetic field on relative gravity determinations with invar pendulums
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 288-296
-
- Article
- Export citation
The reflection of electrons from standing light waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-300
-
- Article
- Export citation
A study of the intensity variations of downcoming wireless waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-318
-
- Article
- Export citation
Front matter
PSP volume 29 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 29 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

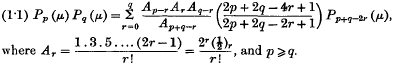
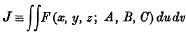
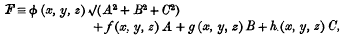
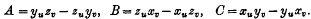
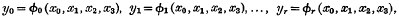
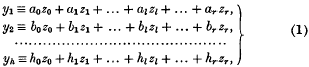
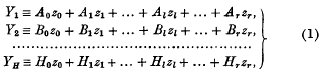
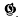 be any transitive permutation group on the
be any transitive permutation group on the 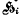 be the subgroup of
be the subgroup of 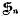 on 1, …,
on 1, …,