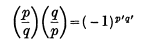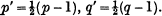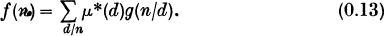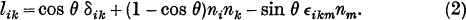Research Article
The Programming of Digital Computers for Sixth Forms
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 117-126
-
- Article
- Export citation
Beginning Mechanics
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 126-131
-
- Article
- Export citation
The Shropshire Mathematics Experiment
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 132-135
-
- Article
- Export citation
Stellations of the Triakis Tetrahedron
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 135-143
-
- Article
- Export citation
Pantactic Squares
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 144-152
-
- Article
- Export citation
Gradient of xn, When N is a Positive Integer: Extension to Cases of N Negative or Fractional
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 153-154
-
- Article
- Export citation
Other
A New Numerical Method of Solving a Space Triangle
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 155-160
-
- Article
- Export citation
Research Article
On Inequalities Connecting Arithmetic Means and Geometric Means of Two Sets of Three Positive Numbers
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 160-162
-
- Article
- Export citation
A Direct Method of Determining the Axis, Focus, Directrix, of a Parabola
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 163-165
-
- Article
- Export citation
A Note on Solutions of the Equations Dnx±x = 0
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 166-168
-
- Article
- Export citation
A Proof of the Law of Reciprocity for Jacobi Symbols
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 169-170
-
- Article
- Export citation
On the Inversion Property of the Mobius’ μ-Function II
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 171-178
-
- Article
- Export citation
The Simple Iterative Method Applied to a Matrix Which has a Dominant Double Real Eigenvalue
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 179-184
-
- Article
- Export citation
Inversion of Nearly Diagonal Matrices
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 184-189
-
- Article
- Export citation
Exponents: A Suggested Replacement for the Standard Treatment
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 189-191
-
- Article
- Export citation
Orthogonal Matrices in Three Dimensions
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 192-194
-
- Article
- Export citation
Other
Corrigendum
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 194
-
- Article
- Export citation
Class Room Notes
130. In the triangle ABC, given a, b abd C; required to find c
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 195-197
-
- Article
- Export citation
131. Mathematical Marriages
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 197-198
-
- Article
- Export citation
Mathematical Notes
3121. A Geometric Proof of a Famous Identity
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 198-200
-
- Article
- Export citation

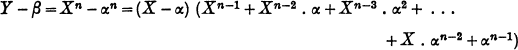
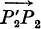 (the height at
(the height at 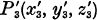 in which the perpendicular form
in which the perpendicular form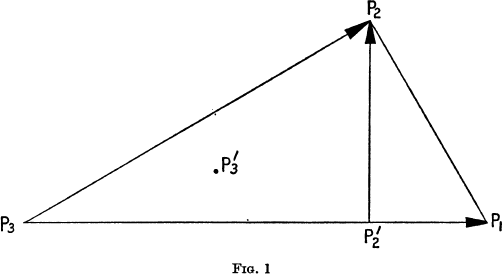
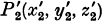 of the given point
of the given point