No CrossRef data available.
Article contents
A Proof of the Law of Reciprocity for Jacobi Symbols
Published online by Cambridge University Press: 03 November 2016
Extract
The congruence x2 ≡ a (mod p), where p is an odd prime and a is any number not divisible by p, sometimes has a solution, but sometimes it has not. Gauss’s symbol (a/p), also known as Legendre’s symbol, is defined as (a/p) = l if there exists at least one x as a solution to this congruence and (a/p) = − l if no such solution exists.
The “Law of Reciprocity”, the famous theorem by Gauss, then states that, if p and q are odd primes,
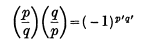
where 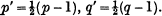
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1965


