No CrossRef data available.
Article contents
Sums of distinct fifth roots of unity and the regular dodecahedron
Published online by Cambridge University Press: 12 November 2024
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Integer linear combinations of cube, fourth, or sixth roots of unity form lattices in the complex plane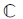 
. In contrast, integer linear combinations of fifth roots of unity do not form a lattice; in fact, they are dense in 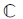. Nevertheless, the geometry for fifth roots of unity has considerable structure. Here we consider only sums of distinct fifth roots of unity, and show that 20 of these sums are orthogonal projections of the vertices of a regular dodecahedron. Pentagonal symmetry here is only to be expected, but it is a little surprising to encounter a plane projection of a polyhedron with much richer dodecahedral symmetry.
- Type
- Articles
- Information
- Copyright
- © The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association
References
Ireland, K. and Rosen, M., A classical introduction to modern number theory (2nd edn.), Graduate Texts in Mathematics 84, Springer (1998).Google Scholar
Stewart, I. and Tall, D. O., Algebraic number theory and Fermat’s last theorem (4th edn.), CRC Press (2015).CrossRefGoogle Scholar
Nguyen, N. P., A note on cyclotomic integers, accessed March 2024 at https://arxiv.org/ftp/arxiv/papers/1706/1706.05390.pdf
Google Scholar
Buhler, J., Butler, S., De Launey, W. and Graham, R., Origami rings, J. Austral. Math. Soc. 92 (2012) pp. 299–311.CrossRefGoogle Scholar
Regular dodecahedron, Wikipedia, accessed March 2024 at en.wikipedia.org/wiki/Regular_dodecahedron.Google Scholar
You have
Access