Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-26T01:28:11.412Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple series representation for Apéry's constant

Published online by Cambridge University Press:  23 January 2015

John Melville
John Melville*
Affiliation:
56 North Meggetland, Edinburgh EH14 1XQ
Get access Rights & Permissions [Opens in a new window]

Extract

Apéry's constant is the value of ζ (3) where ζ is the Riemann zeta function. Thus

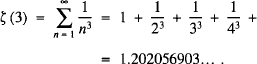
This constant arises in certain mathematical and physical contexts (in physics for example ζ (3) arises naturally in the computation of the electron's gyromagnetic ratio using quantum electrodynamics) and has attracted a great deal of interest, not least the fact that it was proved to be irrational by the French mathematician Roger é and named after him. See [1,2].

Numerous series representations have been obtained for ζ (3) many of which are rather complicated [3]. é used one such series in his irrationality proof. It is not known whether ζ (3) is transcendental, a question whose resolution might be helped by a study of an appropriate series representation of ζ (3).

Type
Articles
Information
The Mathematical Gazette , Volume 97 , Issue 540 , November 2013 , pp. 455 - 460
Copyright
Copyright © The Mathematical Association 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Apéry, Roger, Irrationalite de ζ(2) and ζ(3), Astérisque 61 (1979), pp.11–13.Google Scholar
2. van der Poorten, A., A proof that Euler missed … Apéry's proof of the irrationality of ζ (3), The Mathematical Intelligencer 1 (4), (1979), pp.196–203.Google Scholar
3. Finch, S. R., Mathematical constants, Cambridge University Press (2003), pp. 40–43.Google Scholar