Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T12:28:18.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Patterns among square roots of the 2 × 2 identity matrix

Published online by Cambridge University Press:  15 February 2024

Howard Sporn
Howard Sporn*
Affiliation:
Department of Mathematics and Computer Science, Queensborough Community College, Bayside, NY, USA 11364 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 2 × 2 identity matrix, 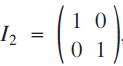$${I_2} = \left( \begin{gathered}{\rm{1 \,\,\,0}} \hfill \\{\rm{0 \,\,\,1}} \hfill \\ \end{gathered}\right)$$, has an infinite number of square roots. The purpose of this paper is to show some interesting patterns that appear among these square roots. In the process, we will take a brief tour of some topics in number theory, including Pythagorean triples, Eisenstein triples, Fibonacci numbers, Pell numbers and Diophantine triples.

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 571 , March 2024 , pp. 84 - 93
Check for updates
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

References

Gomes, L. T., Pythagorean triples explained with central squares, Australian Senior Mathematics Journal 29 (2015) pp. 7–15.Google Scholar
Mitchell, D. W., Using Pythagorean triples to generate square roots of I 2 , Math. Gaz. 87 (2003) pp. 499–500.CrossRefGoogle Scholar
Gordon, R. A., Properties of Eisenstein triples, Mathematics Magazine (2012) pp. 12–25.CrossRefGoogle Scholar
Willson, W. W., A generalisation of a property of the 4, 5, 6 triangle, Math. Gaz. 60 (1976) pp. 130–131.CrossRefGoogle Scholar
Luthar, R. S., Integer-sided triangles with one angle twice another, College Mathematics Journal 15 (1984) pp. 55–56.CrossRefGoogle Scholar
Lord, N., A Striking Property of the (2, 3, 4) triangle, Math. Gaz. 82 (1998) pp. 93–94.CrossRefGoogle Scholar
Mitchell, D. W., The 2:3:4, 3:4:5, 4:5:6 and 3:5:7 triangles, Math. Gaz. 92 (2008) pp. 317–319.CrossRefGoogle Scholar
Koshy, T., Fibonacci and Lucas numbers with applications Wiley (2001).CrossRefGoogle Scholar
Sporn, H., Group structure on the golden triples, Math. Gaz. 105 (2021) pp. 87–97.CrossRefGoogle Scholar
Beardon, A. F. and Deshpande, M. N., Diophantine triples, Math. Gaz. 86 (2002) pp. 258–261.CrossRefGoogle Scholar