No CrossRef data available.
Published online by Cambridge University Press: 23 January 2015
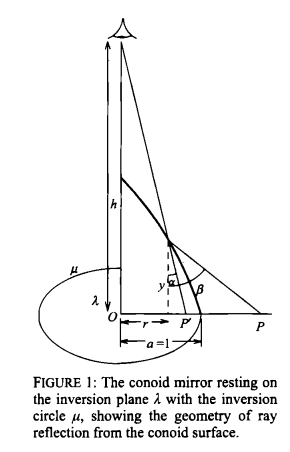
In 1979 Philip W. Kuchel published a paper [1] in the Mathematical Gazette on using curved mirrors as a means of demonstrating the transformation known as inversion in a circle. He called the mirrors ‘anamorphoscopes’ since he came to the idea as a special case of the conical mirror anamorphosis which was a popular optical toy from the seventeenth century onwards [2]. In this paper we revisit his ideas with current technology and provide some extensions to Kuchel's derivation.