Published online by Cambridge University Press: 01 August 2016
While reading a book by David Wells on curious and interesting geometry, I came across the following remarkable theorem named after Holditch.
In Figure 1 the point R divides a straight stick ST into lengths p and q, where p, q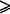 0. We restrict the end points of the stick, S and T, to lie on a plane, simple, closed, convex contour, C1, and ST slides around C1. Assuming C1 is such that ST can pass around C1 once, the locus of R is another plane closed contour, C, inside C1.
0. We restrict the end points of the stick, S and T, to lie on a plane, simple, closed, convex contour, C1, and ST slides around C1. Assuming C1 is such that ST can pass around C1 once, the locus of R is another plane closed contour, C, inside C1.
