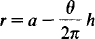Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T15:56:20.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Video tapes

Published online by Cambridge University Press:  01 August 2016

W. B. Macro
W. B. Macro*
Affiliation:
1 Elmfield Gardens, Newcastle upon Tyne NE3 4XB
Get access Rights & Permissions [Opens in a new window]

Extract

Over the years there have been various articles in the Gazette [1, 2, 3] concerning the running time of cassette tapes, but none of them uses the property described here, although it is relevant to all of them.

Let us assume that the revolution counter on a cassette or video recorder is operated by the run off spool. Let a be the radius of the full spool and r the radius when an angle θ radians has been unwound. Rather as in [2] it is clear that a reasonable continuous model of this situation satisfies the equation

Type
Research Article
Information
The Mathematical Gazette , Volume 74 , Issue 468 , June 1990 , pp. 129 - 131
Copyright
Copyright © The Mathematical Association 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Cundy, H.M., Getting it taped I, Math. Gaz. 55 (1971), 43–47.Google Scholar
2. Higgins, J., Getting it taped II, Math. Gaz. 55 (1971), 47–48.Google Scholar
3. Budden, Frank, Cassette tapes, Math. Gaz. 63 (1979), 113–116.Google Scholar