Article contents
Nilpotent-independent sets and estimation in matrix algebras
Published online by Cambridge University Press: 01 May 2015
Abstract
Efficient methods for computing with matrices over finite fields often involve randomised algorithms, where matrices with a certain property are sought via repeated random selection. Complexity analyses for such algorithms require knowledge of the proportion of relevant matrices in the ambient group or algebra. We introduce a method for estimating proportions of families 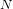 $N$ of elements in the algebra of all
$N$ of elements in the algebra of all 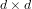 $d\times d$ matrices over a field of order
$d\times d$ matrices over a field of order  $q$, where membership of a matrix in
$q$, where membership of a matrix in 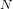 $N$ depends only on its ‘invertible part’. The method is based on the availability of estimates for proportions of certain non-singular matrices depending on
$N$ depends only on its ‘invertible part’. The method is based on the availability of estimates for proportions of certain non-singular matrices depending on 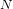 $N$, so that existing estimation techniques for non-singular matrices can be used to deal with families containing singular matrices. As an application, we investigate primary cyclic matrices, which are used in the Holt–Rees MEATAXE algorithm for testing irreducibility of matrix algebras.
$N$, so that existing estimation techniques for non-singular matrices can be used to deal with families containing singular matrices. As an application, we investigate primary cyclic matrices, which are used in the Holt–Rees MEATAXE algorithm for testing irreducibility of matrix algebras.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015
References
- 1
- Cited by


