Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-08T17:35:55.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermodynamic properties of thermonuclear fuel in inertial confinement fusion

Published online by Cambridge University Press:  31 August 2016

V. Brandon ,
B. Canaud ,
M. Temporal  and
R. Ramis
V. Brandon
Affiliation:
CEA, DIF, F-91297 Arpajon, France
B. Canaud*
Affiliation:
CEA, DIF, F-91297 Arpajon, France
M. Temporal
Affiliation:
Centre de Mathématiques et de Leurs Applications, ENS Cachan and CNRS, UniverSud, 61 Avenue du Président Wilson, F-94235 Cachan Cedex, France
R. Ramis
Affiliation:
ETSIA, Universidad Politécnica de Madrid, 28040 Madrid, Spain
*
Address correspondence and reprint requests to: B. Canaud, CEA, DIF, F-91297 Arpajon, France. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hot-spot path in the thermodynamic space 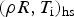$({\rm \rho} R,T_{\rm i} )_{{\rm hs}} $ is investigated for direct-drive scaled-target family covering a huge interval of kinetic energy on both sides of kinetic threshold for ignition. Different peak implosion velocities and two initial aspect ratios have been considered. It is shown that hot spot follows almost the same path during deceleration up to stagnation whatever the target is. As attended, after stagnation, a clear distinction is done between non-, marginally-, or fully igniting targets. For the last, ionic temperature can reach very high values when the thermonuclear energy becomes very high.

Keywords

Direct drive fusionHot-spotHydrodynamics calculationsInertial confinement fusion
Type
Research Article
Information
Laser and Particle Beams , Volume 34 , Issue 3 , September 2016 , pp. 539 - 544
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amendt, P., Landen, O.L., Robey, H.F., Li, C.K. & Petrasso, R.D. (2010). Plasma barodiffusion in inertial-confinement-fusion implosions: application to observed yield anomalies in thermonuclear fuel mixtures. Phys. Rev. Lett. 105, 115005.CrossRefGoogle ScholarPubMed
Amendt, P., Wilks, S.C., Bellei, C., Li, C.K. & Petrasso, R.D. (2011). The potential role of electric fields and plasma barodiffusion on the inertial confinement fusion database. Phys. Plasmas 18, 056308.CrossRefGoogle Scholar
Atzeni, S. & Meyer-ter-Vehn, J. (2004). The physics of inertial fusion. Oxford: Clarendon Press-Oxford.CrossRefGoogle Scholar
Basko, M. (1995). On the scaling of the energy gain of ICF targets. Nucl. Fusion 35, 87.CrossRefGoogle Scholar
Basko, M. & Johner, J. (1998). Ignition energy scaling of inertial confinement fusion targets. Nucl. Fusion 38, 1779.CrossRefGoogle Scholar
Bel'kov, S.A., Bondarenko, S.V., Vergunova, G.A., Garanin, S.G., Gus'kov, S.Y., Demchenko, N.N., Doskoch, I.Y., Kuchugov, P.A., Zmitrenko, N.V., Rozanov, V.B., Stepanov, R.V. & Yakhin, R.A. (2015). Thermonuclear targets for direct-drive ignition by a Megajoule laser pulse. J. Exp. Theor. Phys. 121, 686–698.CrossRefGoogle Scholar
Bellei, C., Amendt, P.A., Wilks, S.C., Haines, M.G., Casey, D.T., Li, C.K., Petrasso, R. & Welch, D.R. (2013). Species separation in inertial confinement fusion fuels. Phys. Plasmas 20, 012701.CrossRefGoogle Scholar
Betti, R., Anderson, K., Goncharov, V.N., McCrory, R.L., Meyerhofer, D.D., Skupsky, S. & Town, R. (2002). Deceleration phase of inertial confinement fusion implosions. Phys. Plasmas 9, 2277.CrossRefGoogle Scholar
Brandon, V., Canaud, B., Laffite, S., Temporal, M. & Ramis, R. (2013a). Marginally igniting direct-drive target designs for the laser Megajoule. Laser Part. Beams 31, 141.CrossRefGoogle Scholar
Brandon, V., Canaud, B., Laffite, S., Temporal, M. & Ramis, R. (2013b). Systematic analysis of direct-drive baseline designs for shock ignition with the laser Megajoule. EPJ: Web Conf. 59, 03004.Google Scholar
Brandon, V., Canaud, B., Temporal, M. & Ramis, R. (2014). Low initial aspect-ratio direct-drive target designs for shock- or self-ignition in the context of the laser Megajoule. Nucl. Fusion 54, 083016.CrossRefGoogle Scholar
Caillabet, L., Canaud, B., Salin, G., Mazevet, S. & Loubeyre, P. (2011a). Change in inertial confinement fusion implosions upon using an ab initio multiphase DT equation of state. Phys. Rev. Lett. 107, 115004.CrossRefGoogle ScholarPubMed
Caillabet, L., Mazevet, S. & Loubeyre, P. (2011b). Multi-phases equation of state of hydrogen from ab-initio calculations in the range 0.2 to 5 g/CC up to 10 eV. Phys. Rev. B 83, 094101.CrossRefGoogle Scholar
Canaud, B., Fortin, X., Garaude, F., Meyer, C., Philippe, F., Temporal, M., Atzeni, S. & Schiavi, A. (2004). High gain direct-drive target design for the laser Megajoule. Nucl. Fusion 44, 1118.CrossRefGoogle Scholar
Canaud, B. & Garaude, F. (2005). Optimization of laser-target coupling efficiency for direct drive laser fusion. Nucl. Fusion 45, L43.CrossRefGoogle Scholar
Canaud, B., Garaude, F., Clique, C., Lecler, N., Masson, A., Quach, R. & Van der Vliet, J. (2007). High-gain direct-drive laser fusion with indirect drive beam layout of laser Mégajoule. Nucl. Fusion 47, 1652.CrossRefGoogle Scholar
Canaud, B. & Temporal, M. (2010). High-gain shock ignition of direct-drive ICF targets for the laser Mégajoule. New J. Phys. 12, 043037.CrossRefGoogle Scholar
Canaud, B., Temporal, M. & Laffite, S. (2012). 2D analysis of direct-drive shock-ignited HiPER-like target implosions with the full laser megajoule for the laser Megajoule. Laser Part. Beams 30, 183.CrossRefGoogle Scholar
Cheng, B., Kwan, T.J.T., Wang, Y.-M. & Batha, S.H. (2013). Scaling laws for ignition at the National Ignition facility from first principles. Phys. Rev. E 88, 041101.CrossRefGoogle ScholarPubMed
Demchenko, N.N., Doskoch, I.Y.A., Gus'kov, S.Y., Kuchugov, P.A., Rozanov, V.B., Stepanov, R.V., Vergunova, G.A., Yakhin, R.A. & Zmitrenko, N.V. (2015). Irradiation asymmetry effects on the direct drive targets compression for the megajoule laser facility. Laser Part. Beams 33, 655.CrossRefGoogle Scholar
Falize, E., Bouquet, S. & Michaut, C. (2009). Scaling laws for radiating fluids: the pillar of laboratory astrophysics. Astrophys. Space Sci. 322, 107.CrossRefGoogle Scholar
Falize, E., Michaut, C. & Bouquet, S. (2011). Similarity properties and scaling laws of radiation hydrodynamic flows in laboratory astrophysics. Astrophys. J. 730, 96.CrossRefGoogle Scholar
Glebov, V.Y., Forrest, C., Knauer, J.P., Pruyne, A., Romanofsky, M., Sangster, T.C., Shoup, M.J. III, Stoeckl, C., Caggiano, J.A., Carman, M.L., Clancy, T.J., Hatarik, R., McNaney, J. & Zaitseva, N.P. (2012). Testing a new NIF neutron time-of-flight detector with a bibenzyl scintillator on OMEGA. Rev. Sci. Instrum. 83, 10D309.CrossRefGoogle ScholarPubMed
Glebov, V.Yu, Sangster, T.C., Stoeckl, C., Knauer, J.P., Theobald, W., Marshall, K.L., Shoup, M.J. III, Buczek, T., Cruz, M., Duffy, T., Romanofsky, M., Fox, M., Pruyne, A., Moran, M.J., Lerche, R.A., McNaney, J., Kilkenny, J.D., Eckart, M.J., Schneider, D., Munro, D., Stoeffl, W., Zacharias, R., Haslam, J.J., Clancy, T., Yeoman, M., Warwas, D., Horsfield, C.J., Bourgade, J.-L., Landoas, O., Disdier, L., Chandler, G.A. & Leeper, R.J. (2010). The National Ignition Facility neutron time-of-flight system and its initial performance. Rev. Sci. Instrum. 81, 10D325.CrossRefGoogle ScholarPubMed
Glebov, V.Yu, Stoeckl, C., Sangster, T.C., Roberts, S., Schmid, G.J., Lerche, R.A. & Moran, M.J. (2004). Prototypes of National Ignition Facility neutron time-of-flight detectors tested on OMEGA. Rev. Sci. Instrum. 75, 3559.CrossRefGoogle Scholar
Herrmann, M., Tabak, M. & Lindl, J. (2001a). A generalized scaling law for the ignition energy of inertial confinement fusion capsules. Nucl. Fusion 41, 99.CrossRefGoogle Scholar
Herrmann, M., Tabak, M. & Lindl, J. (2001b). Ignition scaling laws and their application to capsule design. Phys. Plasmas 8, 2296.CrossRefGoogle Scholar
Hurricane, O.A., Callahan, D.A., Casey, D.T., Celliers, P.M., Cerjan, C., Dewald, E.L., Dittrich, T.R., Doppner, T., Hinkel, D.E., Berzak-Hopkins, L.F., Kline, J.L., Pape, S.L., Ma, T., MacPhee, A.G., Milovich, J.L., Pak, A., Park, H.S., Patel, P.K., Remington, B.A., Salmonson, J.D., Springer, P.T. & Tommasini, R. (2014). Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343–348.CrossRefGoogle Scholar
Inglebert, A., Canaud, B. & Larroche, O. (2014). Species separation and neutron yield modification in inertial-confinement fusion. Eur. Phys. Lett. 107, 65003.CrossRefGoogle Scholar
Kemp, A., Meyer-ter-Vehn, J. & Atzeni, S. (2001). Stagnation pressure of imploding shells and ignition energy scaling of inertial confinement fusion targets. Phys. Rev. Lett. 86, 3336.CrossRefGoogle ScholarPubMed
Levedhal, W. & Lindl, J. (1997). Energy scaling of inertial confinement fusion targets for ignition and high gain. Nucl. Fusion 37, 165.CrossRefGoogle Scholar
Lindl, J. (1995). Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2, 3933.CrossRefGoogle Scholar
Lobatchev, V. & Betti, R. (2000). Ablative stabilization of the deceleration phase rayleigh-taylor instability. Phys. Rev. Lett. 85, 4522.CrossRefGoogle ScholarPubMed
Murakami, M. & Iida, S. (2002). Scaling laws for hydrodynamically similar implosions with heat conduction. Phys. Plasmas 9, 2745.CrossRefGoogle Scholar
Piriz, A.R. (1996). Scaling Laws for the ignition of deuterium-tritium shell targets. Fusion Eng. Des. 32&33, 561.Google Scholar
Recoules, V., Lambert, F., Decoster, A., Canaud, B. & Clerouin, J. (2009). Ab initio determination of thermal conductivity of dense hydrogen plasmas. Phys. Rev. Lett. 102, 075002.CrossRefGoogle ScholarPubMed
Rinderknecht, H.G., Rosenberg, M.J., Li, C.K., Hoffman, N.M., Kagan, G., Zylstra, A.B., Sio, H., Frenje, J.A., Gatu Johnson, M., Séguin, F.H., Petrasso, R.D., Amendt, P., Bellei, C., Wilks, S., Delettrez, J., Glebov, V.Y., Stoeckl, C., Sangster, T.C., Meyerhofer, D.D. & Nikroo, A. (2015). Ion thermal decoupling and species separation in shock-driven implosions. Phys. Rev. Lett. 114, 025001.CrossRefGoogle ScholarPubMed