Shock Hugoniot Data for Water up to 5 Mbar Obtained with Quartz Standard at High-Energy Laser Facilities

Abstract

In this work, we present experimental results on the behavior of liquid water at megabar pressure. The experiment was performed using the HIPER (High-Intensity Plasma Experimental Research) laser facility, a uniaxial irradiation chamber of GEKKO XII (GXII) at the Institute of Laser Engineering (ILE), and the PHELIX at GSI (GSI Helmholtz Centre for Heavy Ion Research), a single-beam high-power laser facility, to launch a planar shock into solid multilayered water samples. Equation-of-state data of water (H₂O are obtained in the pressure range 0.50–4.6 Mbar by tuning the laser-drive parameters. The Hugoniot parameters (pressure, density, etc.) and the shock temperature were simultaneously determined by using VISAR and SOP as diagnostic tools and quartz as the standard material for impedance mismatch experiments. Finally, our experimental results are compared with hydrodynamic simulations tested with different equations of state, showing good compatibility with tabulated SESAME tables for water.

1. Introduction

Equation of state (EOS) of matter at extreme thermodynamic states is of relevance for several fields in physics, especially in laboratory astrophysics and in inertial confinement fusion (ICF), where precise knowledge of the EOS is required. Water is predicted to be abundant in the outer planets of the Solar System, as well as in many of the recently discovered exoplanets. In particular, it is one of the principal ingredients of the mantles of giant planets such as Uranus, Neptune, and Jupiter [1]. The observation of large and asymmetric magnetic fields in these planets [2–4] indicated that the mantle is the origin of the field. As the dynamo theory requires the presence of a conductive material, it was suggested that one or all of the main ingredients of the mantle (ammonia, water, and methane, i.e., carbon [5, 6]) experience a phase transition to a conducting state. Pioneering theoretical work has been done calculating the properties of the superionic phase of water at planetary conditions [7–9]. Therefore, water at very high pressures has been extensively studied in recent works [8, 10–14]. Recently [15, 16], the superionic phase of water was detected experimentally along the Uranus and Neptune isentropes at about 1.5 Mbar by laser shocking water samples precompressed up to 28 kbar. The new superionic phase is predicted to span the pressure range of 1.5 to 6 Mbars.

Superionic water is a solid system that has high ionic conductivity well below the melting temperature. Whether H₂O in planetary interiors is in the superionic or metallic state is of great importance for understanding the source of the planetary magnetic field.

Laser-driven shock compression is a useful technique for generating high pressure and temperature conditions similar to the inner part of Neptune and Uranus. However, measuring P − ρ − T simultaneously is challenging, particularly temperature, as this requires absolute intensity measurements which are not necessary for the determination of the pressure or the density. In this work, we conducted laser-driven shock experiments on H₂O samples up to 4.6 Mbar; along with pressure and density, we evaluated the temperature from measured reflectivity and thermal emission of the shocked sample.

The impedance mismatch (IM) method is widely used for the determination of Hugoniot of sample material. Given that one knows Hugoniot of a “standard” material that is used as a reference, the Rankine–Hugoniot (RH) [17] set of equations, expressing the conservation laws, can be used to relate the experimentally measured shock velocity (D _s ) in the standard material before the shock reaches the standard-sample interface in the sample after it passes through the interface. In this work, we used z-cut α-quartz (SiO₂) as a reference material [18, 19] which, at ambient pressure, is transparent to visible light and becomes reflective at pressures above 1 Mbar [20]. As diagnostic tools, we used the velocity interferometer system for any reflector (VISAR) [21–25] which allowed us to make a precise measurement of shock wave parameters and characterize the EOS of water. The RH set provides information of P and ρ, but not of T, whereas T is also an important thermodynamic parameter. Indeed, in this work, we also measured the temperature using streaked optical pyrometry (SOP) diagnostic data.

2. Experimental Setup

2.1. GEKKO XII-ILE Laser Facility

The first experiment was carried out on the HIPER (High-Intensity Plasma Experimental Research) laser facility, a uniaxial irradiation chamber of the GEKKO XII (GXII) laser at the Institute of Laser Engineering (ILE), Osaka University. Up to 12 beams of neodymium-doped yttrium aluminum garnet (Nd:YAG) laser, frequency tripled (351 nm), were used in the experiment. The laser pulse temporal profile was approximately square shape in time with full width at half maximum (FWHM) 2.5 ns with typical rise and fall time of 100 ps each. The focal spot diameter was 600 µm flat top. SSD (smoothing by spectral dispersion technique) was applied to smooth out the beams. Kinoform phase plates were also used to achieve uniform irradiation, resulting in good shock front planarity.

Figure 1 shows the experimental setup and target configuration. A typical target assembly consisting of 10 µm parylene (C₈H₈) will be referred to as CH/200 nm Au/100 µm quartz (with AR@1054&532 both sides) nominally, ∼500 µm water/100 µm quartz (with AR@1054&532 both sides). The laser initially hits the 0.1 µm-thick Al layer, coated over the CH layer, to avoid laser shine through. The CH layer is the actual ablator, and quartz is the pusher layer. The 200 nm gold layer was placed to stop any X-rays from the plasma corona and avoid preheating of water. Water cells were produced at the Technical University of Darmstadt (Germany) target fabrication department. Due to the low Z ablator and the low laser intensity, X-ray radiation is low and characterized by low photon energy. The Au layer is capable to stop the X-ray radiation; thus, preheating of water is negligible.

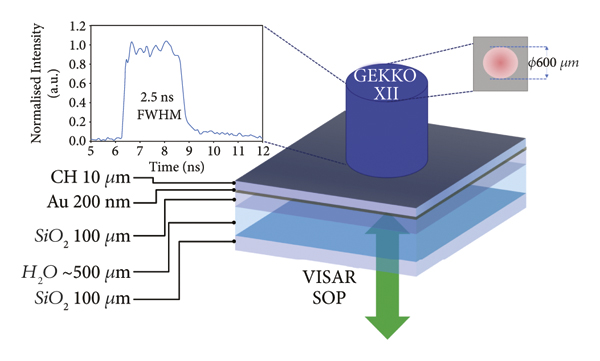
Figure 1: Experimental setup: sketch of the multilayered target design in planar geometry with its associated thicknesses used in our experiment. Drive laser from top. From bottom, the VISAR and SOP measure the shock velocity and the self-emission of the shocked sample on the rear side.

The primary diagnostics were the VISAR and SOP. Two line-imaging interferometers (VISARs) allow to record time-resolved Doppler shift of the velocity of the fast-moving reflector and also the optical properties such as reflectivity [21–26]. These VISARs had different velocity-per-fringe (VPF) sensitivities to resolve the 2π-phase jump ambiguities due to the shock velocity jump at material interfaces. The sensitivity of the two VISARs was 7.523 km/s and 4.476 km/s taking into account the refractive index of SiO₂. The VISAR probe beam was an injection-seeded Q-switched YAG laser. The pulse duration of the probe was ∼10 ns at the FWHM, and its wavelength was 532 nm. The postprocessing of the VISAR raw data obtained in the experiment allows determining [27] the fringe position to 10% of a fringe, while the multiple fringe shifts allow the precision of the shock velocity measurements to be a few percent. Our VISAR analysis showed uncertainties in measured D _s of the order of 3%.

To measure the shock temperature, we used SOP [28–30]. The self-emission of the shocked sample at wavelength 450 nm with 38 nm bandwidth was recorded spatially and temporally resolved, using an absolutely calibrated SOP.

2.2. PHELIX-GSI Laser Facility

The second experiment was conducted at the GSI facility using the PHELIX laser, a flash-lamp-pumped Nd:glass laser utilizing the second harmonic at wavelength 527 nm. The spatial profile was flat top with spot 350 µm FWHM obtained by an appropriate phase plate [31], and the temporal profile was top hat with a duration of 3.5 ns (FWHM). The laser was focused onto a multilayered target with intensity I 5.49 × 10¹² W/cm² to 2.52 × 10¹³ W/cm². The ablation pressure was approximately 12 Mbar, was generated in our plastic ablator (parylene with gross chemical formula C₈H₈), and was estimated from the well-known scaling laws [32–34] for given intensities.

(1) $\begin{array}{}P=8.6{\left(\frac{I}{{10}^{14}}\right)}^{2/3}{\lambda }^{-2/3}{\left(\frac{A}{2Z}\right)}^{1/3},\end{array}$

where A and Z are the atomic mass number and the atomic number of the target material: I is in W/cm², P in Mbar, and λ in μm. A schematic of the PHELIX experimental setup is shown in Figure 2. Targets were also produced at the Technical University of Darmstadt (Germany) target fabrication department.

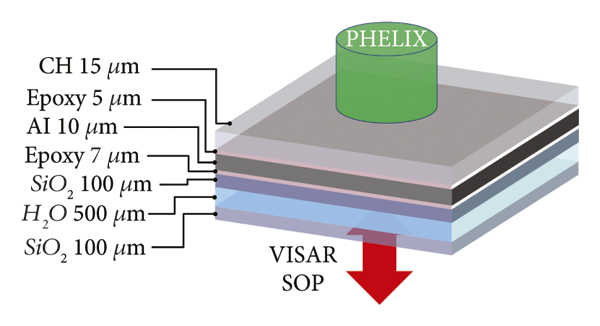
Figure 2: Experimental setup: a sketch of the multilayered target design at the PHELIX laser facility in planar geometry with its associated thicknesses used in our experiment. Drive laser from the top. Bottom: the VISAR and SOP diagnostics which measure the shock velocity and the self-emission of the shocked target on the rear side.

The target configuration and the experimental setup are presented in Figure 2. The sample consists of 15 µm C₈H₈ (parylene)/5 µm epoxy/10 µm Al/7 µm epoxy/100 µm quartz (with AR@1054&527 both sides) nominally, ∼500 µm water/100 µm quartz (with AR@1054&527 both sides). The laser initially hits the 0.1 µm-thick Al layer, coated over the CH layer, to avoid direct laser shine through. Epoxy was used to glue CH/Al and Al/quartz interfaces. The CH layer is the actual ablation layer, and quartz is the pusher layer. The 10 µm Al layer was placed to stop any X-rays from the plasma corona and avoid preheating of the quartz/water layers. The VISAR laser had a wavelength of 660 nm, and the associated sensitivities were 1.285 km/s/f and 4.7 km/s/f, respectively. Also, SOP was looking at the self-emission of the shocked target; however, here, we report only VISAR results and compare with findings on water samples from the GEKKO XII laser facility.

3. Impedance Mismatch Method: Single-Shock Data

The impedance-matching method [5, 17–19, 35] was used to estimate the shock state in water after passing the quartz/water interface; an illustrative method is shown in Figure 3. Because of the impedance mismatch at the SiO₂/H₂O interface, the shock wave produced a transmitted shock into H₂O and a reflected rarefaction wave propagating back into quartz. In the rarefaction wave, the shock-compressed quartz undergoes isentropic release until its pressure and particle velocity match those of shocked water. The IM method requires precise knowledge of Hugoniot and release behavior of the standard reference material (quartz in our case) and the Rankine–Hugoniot (RH) jump relations, which are derived from the conservation laws, mass, momentum, and energy to close the system and derive all the remaining thermodynamic parameters:where ρ,D_s,U_p,P, and ε denote the density, shock velocity, particle velocity, pressure, and internal energy behind the shock. The initial states are denoted with subscript 0. The third equation plotted in the (P − U) plane gives the so-called Rayleigh line of the material. Figure 3 illustrates such a method, deriving the shock pressure in water and the particle velocity. The measurement of $D_s^{Qz}$ gives the shock state $\left(P^{Qz},U_p^{Qz}\right)$ . The crossing of the isentropic release of the quartz standard with the Rayleigh line of the water sample determines the shock state in water $\left(P^{{\text{H}}_2\text{O}},U_p^{{\text{H}}_2\text{O}}\right)$ .

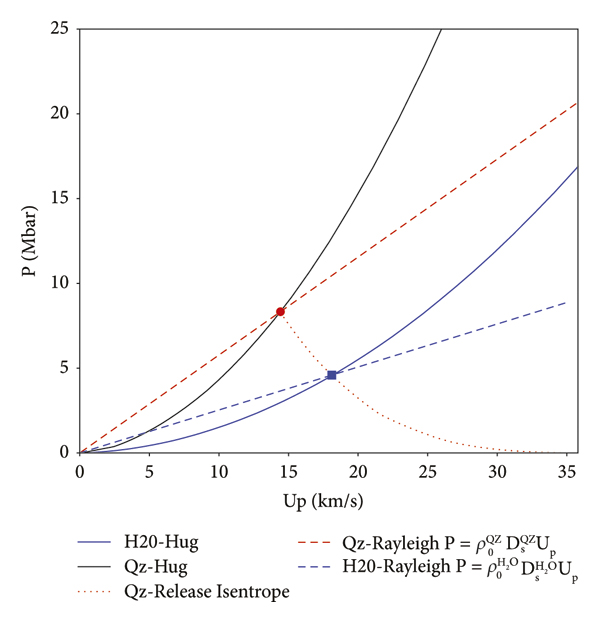
Figure 3: P − U_p graphical construction of the impedance mismatch procedure for the highest pressure shot of the quartz standard. The shocked state of H₂O is constrained to remain on the incident Rayleigh line (blue dashed line) defined for $D_s^{Qz}=21.8\left(\text{km}/\text{s}\right)$ for this case. The solid red and dashed lines are the Hugoniot and the Rayleigh line of (SiO₂), respectively, associated with the release curve calculated for $D_s^{Qz}=21.8\left(\text{km}/\text{s}\right)$ . The crossing of the Rayleigh line with the release isentrope path (blue square) determines the IM point and provides the experimental value of $\left(P^{{\text{H}}_2\text{O}},U_p^{{\text{H}}_2\text{O}}\right)$ which may or may not lay on the shock polar for water, i.e., may (or may not) be in agreement with the used theoretical EOS.

(2) $\begin{array}{}\frac{\rho }{{\rho }_0}=\frac{D_s}{D_s-U_p},\end{array}$

(3) $\begin{array}{}P-P_0={\rho }_0{D}_s{U}_p,\end{array}$

(4) $\begin{array}{}\epsilon -{\epsilon }_0=\frac{1}{2}\left(P+P_0\right)\left(\frac{1}{{\rho }_0}-\frac{1}{\rho }\right).\end{array}$

4. Results and Discussion

Figure 4 presents the raw data obtained with the VISAR for the shot SID-43058. The arrival time of the shock at the Au/SiO₂ interface front side defines the time zero (t ₀ = 0). Then, while the shock front enters into SiO₂, it becomes highly reflective, and its velocity gradually decreases. It is indicated in the raw image with a dotted line as t ₀. At t ₁ = 7.21 ns, the shock front strikes the H₂O layer as shown in Figure 4. The velocity profile and the reflectivity obtained from Figure 4 are shown in Figure 5. The transmitted shock in H₂O also becomes reflective. The shock velocity in SiO₂, used in the impedance mismatch analysis, was obtained by analysing VISAR images first by using shock chronometry, i.e., the average shock velocity in SiO₂ was given by $D_s^{Qz}=100\mu \text{m}/\left(t_1-t_0\right)$ . Then, the analysis is refined by looking at the displacement of the fringe shift and averaging the shock velocities from the two VISAR records taking into account the temporal resolution of the streak camera and the sensitivities of each VISAR. The IM method is applied using the instantaneous value of the shock velocity just before t ₁.

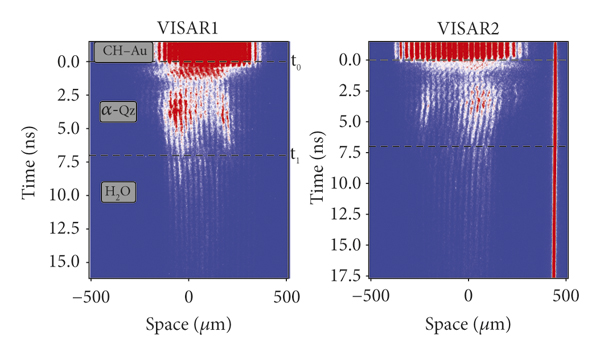
Figure 4: Experimentally obtained VISAR images for the shot SID-43058.

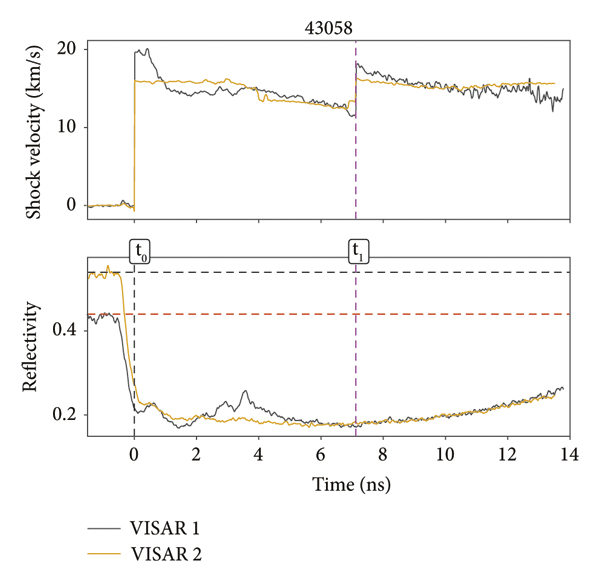
Figure 5: Top: evolution of the shock velocity in time for SiO₂ and H₂O extracted from Figure 4: VISAR-1 (black) and VISAR-2 (yellow). Bottom: the reflectivity vs. time. This shows an increase after the shock enters the SiO₂ layer owing to the reverberating wave in SiO₂ (at about t ≈ 3-4 ns), and a second increase appears when the shock passes the SiO₂-H₂O interface at time t ₁. Shock velocities are listed in Table 1 (SID-43058).

Table 1: Hugoniot data from the impedance mismatch method with α-quartz as a reference material. The velocity of shock in quartz D^Qz and water $D^{{\text{H}}_2\text{O}}$ was used in the IM analysis to obtain the particle velocity $U_p^{{\text{H}}_2\text{O}}$ , pressure $P_{{\text{H}}_2\text{O}}$ , and density ${\rho }_{{\text{H}}_2\text{O}}$ on water Hugoniot. The compressibility ${\left(\rho /{\rho }_0\right)}^{{\text{H}}_2\text{O}}$ was calculated by dividing ${\rho }^{{\text{H}}_2\text{O}}$ by the initial density. Water target was studied at two different high-power laser facilities.

To determine $D_s^{{\text{H}}_2\text{O}}$ , we instead could rely only on the VISAR images. The experimental results were supported with numerical simulation utilizing MULTI-1D, which is a one-dimensional radiation hydrodynamic code [36]. Simulations show that, in the present experiment, $D_s^{Qz}$ decays. We observe a decay in the case of $D_s^{{\text{H}}_2\text{O}}$ . Detailed interpretation of simulations will be shown in Section 6.

Getting Hugoniot points for H₂O requires that one knows the release isentrope (RI) of SiO₂ from its shocked state. This study uses an EOS model to calculate the release isentrope for each shock state in SiO₂ utilizing an in-house Python script. The IM method provides the Hugoniot state of H₂O as the locus where the release isentrope of SiO₂ crosses the Rayleigh line $\left(P={\rho }_0^{{\text{H}}_2\text{O}}{D}_s^{{\text{H}}_2\text{O}}{U}_p\right)$ of water.

Such a method is shown in Figure 3, with the Hugoniot and the RI of SiO₂ (black line and red dotted curve, respectively). Dashed lines denote the Rayleigh lines of SiO₂ and water (red and blue), respectively, as well as their associated Hugoniot. The Hugoniot curve is derived from the SESAME database [37] and the QEOS [38], tabulated data 7385 for quartz and 7154 for water. The obtained shocked states of water are compared with other available works and are shown in Figure 6 in the P − ρ plane and in Figure 7 in the P − U_p plane.

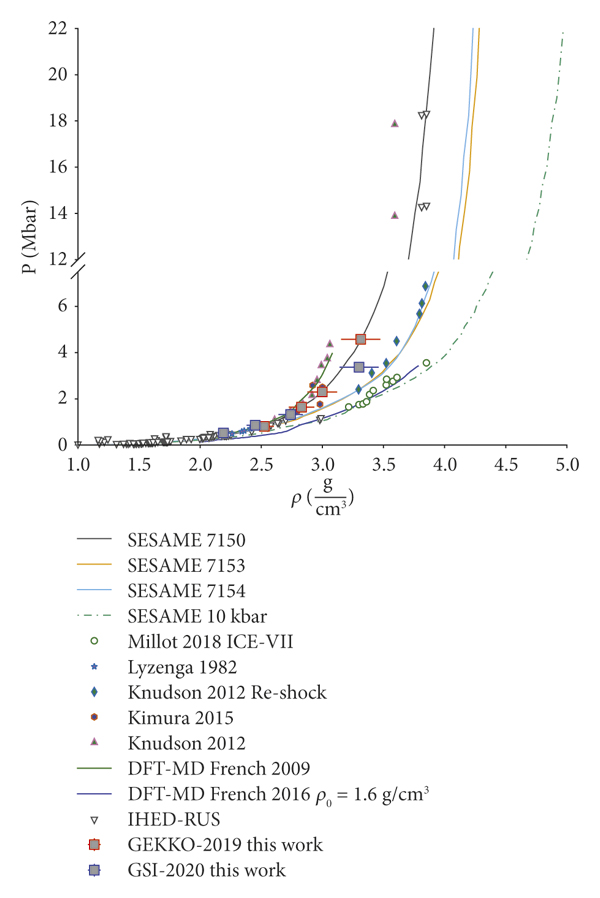
Figure 6: Water Hugoniot data in the P − ρ plane. Squared data points: our experimental points. The lines correspond to tabulated data from SESAME (SESAME 7150, 7153, and 7154 and P ₀ = 10 kbar) [37]. Density functional theory-molecular dynamics (DFT-MD) calculations of Hugoniot of water form French et al. [9, 39].

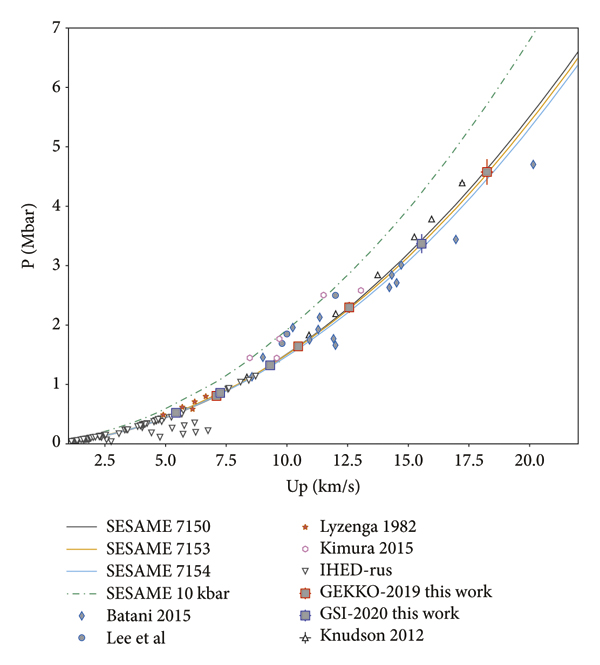
Figure 7: Water Hugoniot data in the P − U_p plane. Our data showed good agreement with the SESAME models available for water.

5. Temperature Measurement

The shock front emits thermal radiation, and which, in our experiment, was collected by the SOP [28, 44]. The absolute spectral radiance of the shock front was measured at a wavelength of 450 nm with bandwidth 38 nm. Assuming a grey body spectrum, the spectral radiance I (450 nm) is given by Planck’s black body emissivity corrected for the absorptivity of the material (ε = 1 − R) calculated using the reflectivity R of the shock front measured by VISARs since the light is either absorbed or reflected. Then,

(5) $\begin{array}{}I\left(\lambda ,T\right)=A\left(\lambda \right)\frac{2h{c}^2}{{\lambda }^5}\frac{1}{e^{hc/\lambda k_{B}T}-1}.\end{array}$

The temperature was determined using this formula (where h, c, and k_B are Planck’s constant, speed of light, and Boltzmann’s constants, respectively). A(λ) is a parameter taking into account the reflectivity, the sensitivity of the streak, the geometry, and the collection optics path.

Solving equation (5) with respect to temperature, we get

(6) $\begin{array}{}T=\frac{hc}{\lambda k_B\ln \left(\left(2h{c}^{2}A\left(\lambda \right)/I\left(\lambda \right){\lambda }^5\right)+1\right)}.\end{array}$

SOP calibration has been made in situ using the quartz standard (GEKKO XII) [42, 45]. For the temperature estimation, we used the mean reflectivity of the two VISAR records which were taken simultaneously for each shot. The results of SOP temperature estimation are shown in Figure 8 where we report two shots at different laser energies with the associated temperature profile in time (Figure 8(a)).

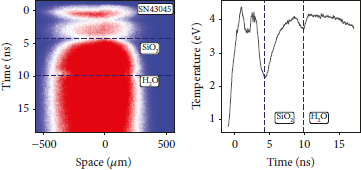
Figure 8: (a) SOP result for shot SN43045 at a laser energy of 1.1 kJ, the highest energy shot obtained in our experiment, and (b) temperature estimation taking into account the mean reflectivity of VISAR-1 and VISAR-2. The initial luminosity (t ≤ 4 ns) is due to scattered laser light.

The temperature results as a function of pressure reaching the water interface are shown in Figure 9 together with results from Lyzenga et al. [41], Kimura et al. [10], and Guarguaglini et al. [42] and Hugoniot tabulated curves based on SESAME models (SESAME 7150, 7153, and 7154 and P ₀ = 10 kbar) and ab initio Hugoniot from French et al. [39].

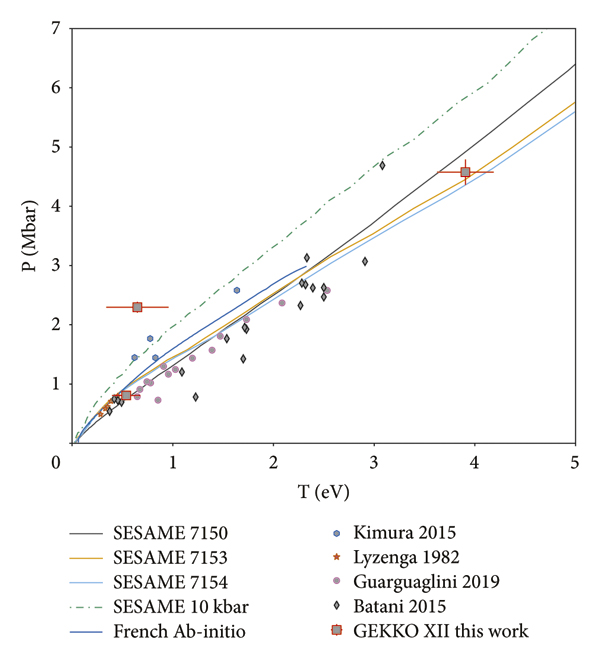
Figure 9: Principal Hugoniot data in the P − T plane obtained in this study from the GEKKO XII-ILE laser facility, compared with Lyzenga et al. [41], Kimura et al. [10], Guarguaglini et al. [42], and Batani et al. [43]. Also shown are SESAME models for three different tabulated EOS data at slightly different initial densities.

6. Hydro Simulations

1D radiative hydrodynamic simulations were performed with MULTI-1D [36] to comprehend our experimental results. The laser temporal profile of the pulse was flat top in time with a plateau duration of 2.5 ns at FWHM and rise and fall times of 0.1 ns. In the simulation, we utilized the SESAME tables of the following materials which consist of our target SESAME table 7770 for parylene [37], SESAME table 2700 for gold [37], SESAME 7385 for quartz [37], and SESAME tables 7150, 7153, and 7154 for water [37]. Concerning the water EOS, we compared different models of EOS tables coming from the SESAME database [37], from QEOS [38], and from FEOS [46], in all cases setting the initial density at ρ ₀ = 0.98 (g/cm³) in order to check the validity of the EOS data. The density and pressure map, reproducing the shot SID-43058 obtained from 1D simulation, is shown in Figures 10(a) and 10(b), respectively. Figure 10(c) shows the change of the maximum density postprocessed from Figure 10(a) at interval times, and Figure 10(d) shows the change of pressure along the shock front of the simulated target top (Figure 10(b)), respectively. The use of 1D simulation to interpret the experimental results is confirmed because of the use of appropriate phase plate resulting in a large focal spot (∼600 µm). In addition to this, the justification of the 1D approximation is supported by two experimental observations; such results can be seen in Figure 4 where good planarity of the shock is observed.

Raw data from VISAR images (see Figure 4) indicate that the shock breakout is quite flat both at metal/SiO₂ and at SiO₂/H₂O interfaces. At this point, we must note that 2D effects will result in curvature, initially affecting the edges of the shock front, yet gradually advancing to the center. However, in our experimental results, the curvature of the shock front is not observed suggesting that the 2D effects in hydrodynamics can be neglected. In our case, the velocity of the shock is maintained and decaying quite slowly, and actually (within error bars), the decay obtained by analysing the VISAR images is compatible with the results of 1D simulations. The reduction of shock pressure and velocity during propagation is caused by two phenomena: (a) the release wave from the target front side catching up the traveling shock and (b) 2D effects in shock front propagation. In fact, due to the fair agreement of conducted experiment with 1D simulations, we conclude that (b) is not important. Indeed, a much faster decay of shock pressure and velocity would be expected if 2D effects were important.

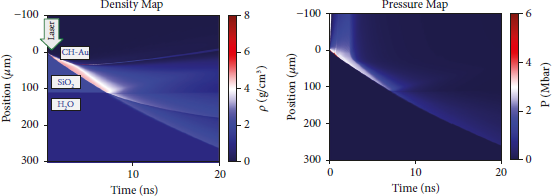
Figure 10: Laser drive beam hits the target from the top as indicated by the arrow symbol; the constituent layers are also indicated with the right order (CH/Au/SiO₂/water). (a) Hydrodynamic progression of the density map obtained from MULTI-1D reproducing the experimental results of shot SID-43058 with nominal laser intensity 1.4 × 10¹³ W/cm²; for this particular shot, 3 beams/12 were used for the main drive delivering a total of 252 J on the target. With the above laser parameter, the simulation reproduces well the shock breakout time in the SiO₂-H₂O inner interface. (b) Variation of the pressure map for the same shot conditions. (c) Time evolution of pressure and density forms MULTI simulation for shot SID-43058. (d) Change of pressure at the shock front up to the maximum simulation time.

7. Conclusion

In summary, we obtained EOS data of water along the principal Hugoniot up to 5 Mbar. Water samples, contained within a multilayered water cell, were dynamically compressed in planar geometry using the high-power laser facilities GEKKO XII (ILE) and PHELIX (GSI). Utilizing quartz as a standard material in both experimental campaigns and the main diagnostics such as VISAR/SOP substantially reduced experimental errors in optimized experimental conditions. The impedance mismatching analysis allowed to verify that P, ρ, (ε − ε ₀, and the Hugoniot data are in fair agreement with those predicted by SESAME table 7150, and on the contrary, they show a significant difference concerning the Hugoniot curve calculated using DFT-MD simulations. Also, our experimental outcome showed good agreement with simulations performed with the radiative hydro code MULTI-1D using the SESAME tabulated EOS, the QEOS model, and the FEOS model, a modified version of the QEOS. The agreement with 1D simulations shows indeed that, in our experimental setup, 2D effects in hydrodynamics are negligible, a result which mainly depends on the use of laser focal spots. For a few shots, we could also measure the temperature of shocked material using calibrated SOP diagnostics. Our data confirm previous experimental results and show that, in the pressure range up to 4.6 Mbar, water is in a reflective state.