Why dyads heed advice less than individuals do

Abstract

Following up on a recent debate, we examined advice taking in dyads compared to individuals in a set of three studies (total N = 303 dyads and 194 individuals). Our first aim was to test the replicability of an important previous finding, namely that dyads heed advice less than individuals because they feel more confident in the accuracy of their initial judgments. Second, we aimed to explain dyads’ behavior based on three premises: first, that dyads understand that the added value of an outside opinion diminishes when the initial pre-advice judgment is made by two judges rather than one judge (given that the dyad members’ opinions are independent of each other); second, that they fail to recognize when the assumption of independence of opinions does not hold; and third, that the resistance to advice commonly observed in individuals persists in groups but is neither aggravated nor ameliorated by the group context. The results of our studies show consistently that previous findings on advice taking in dyads are replicable. They also support our hypothesis that groups exhibit a general tendency to heed advice less than individuals, irrespective of whether the accuracy of their initial judgments warrants this behavior. Finally, based on the three assumptions mentioned above, we were able to make accurate predictions about advice taking in dyads, prompting us to postulate a general model of advice taking in groups of arbitrary size.

1 Introduction

Advice is a simple and often effective means to improve the quality of judgments and decisions (Yaniv, 2004). Accordingly, researchers have studied extensively when and how decision-makers heed advice, and to what extent they benefit from doing so. So far, there is robust evidence that decision-makers can, to some extent, infer the quality of advice from a range of cues, and that they generally benefit from advice in terms of decision quality. However, they do not use advice to its full potential, because they tend to overweight their own initial opinion (for reviews, see Bonaccio & Dalal, 2006; Rader, Soll & Larrick, 2017; Yaniv, 2004). One central limitation of previous research on advice taking is that – despite the great relevance of groups as decision-makers in business and politics – it almost exclusively focuses on individual decision-makers.

In the, as of yet, only published study on advice taking in groups, Minson and Mueller (2012) studied how well dyads – compared to individuals – use advice in the judge-advisor system (JAS; Sniezek & Buckley, 1995). In the JAS, one entity (the judge) first makes an initial judgment, then receives the judgment of another entity (the advisor), and finally provides a – possibly revised – final estimate. Minson and Mueller (2012) found that dyad judges assigned less weight to advice than individual judges did, and this effect was mediated by dyads’ greater confidence in the accuracy of their initial estimates. Interestingly, the initial accuracy of individual and dyad judges did not differ significantly, and any little edge that dyad judges might have had over individuals in terms of accuracy disappeared after receiving advice. Accordingly, Minson and Mueller concluded that groups are less receptive to advice than individuals are, with potentially harmful consequences for decision quality.

Challenging this interpretation, we argued that groups should heed the same advice less than individuals do, because group judgments already contain the input of multiple individuals (Schultze, Mojzisch & Schulz-Hardt, 2013). This reasoning is based on previous findings from research on group judgment showing that groups perform at least as well as the average of their members’ individual judgments (for reviews, see Hastie, 1986; Gigone & Hastie, 1997). Based on the premise that – given comparable expertise of judges and advisors – each opinion of a person involved in the judge-advisor should be treated equally, we derived what we considered the normatively correct a-priori weight of advice. For example, when receiving advice from one advisor, individual judges should weight the advice by 50%. Dyads, in contrast should weight the same advice by only 33%, which amounts to two thirds of the optimal weight for individual judges (see also Mannes, 2009). Our reanalysis of the original data of Minson and Mueller (2012) showed comparable deviations from the optimal weights in individual and dyad judges, leading us to conclude that groups and individuals were equally reluctant to heed advice. In particular, an inspection of the average weight that individual and dyad judges in the original study assigned to the advice further supports our interpretation. The weight of advice in the dyad judge condition was roughly two thirds of the weight individual judges assigned to the advice. Thus, our reanalysis is consistent with the idea that dyad judges not only understood that an outside opinion should be less valuable to a dyad than to an individual but also to what extent this added value decreases.

Responding to our reanalysis and reinterpretation, Minson and Mueller (2013) noted that our argumentation holds only if all persons involved in the JAS contribute independent information. In other words, initial judgments of group judges must resemble an aggregate of the group members’ independent pre-discussion judgments. This is clearly the case in most previous research because the experimental procedure required that group members provide independent estimates prior to discussion. However, the assumption of independence of opinions did not hold in the original study by Minson and Mueller (2012), arguably because the experimental procedure did not entail independent pre-discussion judgments. Accordingly, dyad judges’ initial accuracy fell short of a simple aggregate of two individual judgments. Minson and Mueller (2013) concluded that lower weights of advice in dyads were not justified by greater initial accuracy and that, accordingly, groups were overly resistant to advice.

One important lesson to learn from this debate is that equal weighting of all involved opinions fails to serve as a general normative benchmark of advice taking in dyads – the same is true for always averaging the initial estimate and the advice. Depending on the task and context, judgment accuracy in groups can range from being roughly equal to that of single individuals, as was the case in Minson and Mueller’s (2012) study, to outperforming even an aggregate of a comparable number of individuals (Minson, Mueller & Larrick, 2018; Schultze, Mojzisch & Schulz-Hardt, 2012; see Einhorn, Hogarth & Klempner, 1977, for a formal analysis). This makes it very difficult to state, a priori, how strongly groups should heed advice relative to individuals.

However, by integrating the seemingly contradicting lines of argumentation described above, we can derive a plausible explanation as to why dyads heed advice less than individuals do. This integration goes as follows. First, we assume that dyads share the common belief that “two heads are better than one.” That is, they understand that (and potentially to what extent) the value of an additional opinion depends on whether the initial judgment stems from an individual versus a dyad. Second, however, we assume that dyads are unable to recognize, and correct for, dependencies between their members’ individual contributions. This inability is not entirely surprising if one inspects the sources of within-group dependency. One source is a shared bias towards under- or overestimating the true values (Einhorn et al., 1977). Another source, and this is what Minson and Mueller (2012, 2013) suggested as an explanation for the high interdependence of their dyad judges, is anchoring. Groups (and individuals) are usually not aware of such biases – if they were, they could immediately correct them. Together, the first two assumptions lead to the general intuition that making judgments in dyads results in greater initial accuracy and, accordingly, warrants lower weights of outside advice. Third, and finally, we assume that the resistance to advice commonly observed in individuals (e.g., Gino, Brooks & Schweitzer, 2012; Soll & Larrick, 2009; Yaniv & Kleinberger, 2000) persists in the dyadic context and is neither aggravated nor ameliorated when comparing dyads with individuals. The three assumptions allow us to make the prediction that dyads generally heed advice less than individuals, both when it is justified by greater initial accuracy and when it is not.

The present research pursues two goals. The first is to test whether the results of Minson and Mueller (2012), namely lower weights of advice in dyads compared to individuals mediated by greater confidence, are replicable. Second, we aim to solve the research debate described above. To this end, we test the hypothesis that the lower weights of advice in dyads occur irrespective of whether they are justified by greater initial accuracy.

2 Study 1

Study 1 is an extended replication of the original Minson and Mueller (2012) study. We asked participants to work on a set of fifteen quantitative judgment tasks. Nine of these tasks were German translations of the original tasks used by Minson and Mueller, allowing for a close replication. We added six new judgment tasks to test the hypothesis that lower weights of advice in dyad judges occur irrespective of whether they are warranted by greater initial accuracy. We chose additional tasks so that in some of them we would expect dyads to outperform individuals, whereas in others, we would expect them to perform at a similar level. Other than the percentage estimates used in the original study, which are, by definition, capped at an upper limit of 100%, the new tasks are unbounded; that is, they have no natural upper limit. These tasks allow for more extreme biases (Minson et al., 2018) and, thus, should be well suited to test our hypothesis. Half of the new tasks were tasks with low bias, that is, underestimation and overestimation of the true values was about equally likely, thereby allowing these idiosyncratic biases to cancel each other out. If bias in a task is low, dyad judgments are likely to be more accurate than those of individuals (due to error cancellation) and, ideally, comparable in accuracy to an aggregate of two randomly drawn individual judgments. This creates a situation where lower weights of advice would be justified by greater initial accuracy. The remaining three tasks were characterized by high bias, that is, either (almost) all participants overestimated the true value or (almost) all of them underestimated it. In this case, aggregation of judgments does not lead to error cancellation, and the initial accuracy of dyad judges should not differ substantially from the accuracy of individual judges. Thus, if bias is high, and dyads do not perform better than individuals do, lower weights of advice would not be justified. Based on the descriptive data on initial accuracy provided in the study by Minson and Mueller (2012), we would expect the original tasks to fall in between the extremes that we created with the new tasks. If our reasoning holds true, we would expect task type to moderate the differences in the initial accuracy of individual and dyad judges, whereas the lower weight of advice in dyads should occur irrespective of it.

Note that, although our focus was the comparison of individual and dyad judges, we chose to conduct a replication of Minson and Mueller’s (2012) complete study design. Thus, in Study 1, we also manipulated whether the advisor was an individual or a dyad, allowing us to replicate all aspects of the original study, and in particular, the somewhat puzzling finding that judges seemed not to consider advisor type when making the final estimates.

2.1 Method

2.1.1 Participants and design

Participants were 299 university students. We aimed for roughly 50 individuals or dyads per cell to match the power of the original study by Minson and Mueller (2012). Participants were, on average, 24.58 years old (SD = 5.02); 179 were female (60%), and 120 were male (40%). Study 1 used a 2 (judge type: individual vs. dyad) × 2 (advisor type: individual vs. dyad) × 3 (task type: original vs. low bias vs. high bias) design with judge type and advisor type as between-subjects factors and task type as a within-subjects factor.

2.1.2 Procedure

The procedure mimicked that of the original study (Minson & Mueller, 2012) as closely as possible. Participants worked as individual or dyad judges in the JAS, receiving advice from either individuals or dyads. They were assigned randomly to one of the four conditions. Each individual or dyad worked in a separate room. Participants received written information about the procedure of the study. Specifically, they were informed that they would work on a set of fifteen quantitative judgment tasks twice. First, they would provide their initial judgments. Then they would receive advice in the form of the judgments another individual or dyad had made, while their own initial estimates would also serve as advice for another individual or dyad. After receiving the advice, participants would work on the same tasks a second time to provide their, possibly revised, final estimates. In the instructions, participants learned whether their advisor was an individual participant or a dyad. Participants were also informed that their payment would consist of two components: a fixed participation fee of 5 Euros, and a performance-based bonus. Similar to the original study, participants started with a bonus payment of 30 Euros, which was reduced by 1 Euro for every ten percentage points or for every ten percent (depending on the task) their final estimates deviated from the respective true values.

Nine of the fifteen judgment tasks were German translations of the original percent estimation tasks used by Minson and Mueller (2012), for example, estimating the percentage of households owning pets. The remaining six tasks were unbounded judgment tasks, meaning that, other than the percent estimates, the response scale did not pose an upper limit on the judgments (e.g., estimating the population of Hamburg). From a large pool of judgment tasks, we selected three tasks because pretests had shown that participants’ judgments were, on average, very close to the true values, and overestimations were roughly as frequent as underestimations. That is, these tasks show low population bias. We chose the remaining three tasks because almost all pretest judgments were on the same side of the true value, that is, participants exhibited a strong population bias. The order of the fifteen tasks was randomized once and then held constant for all participants.

Participants first made their initial estimates for all judgment tasks. Consistent with the original study by Minson and Mueller (2012), dyad members did not provide individual judgments prior to discussion. Instead, they immediately discussed the tasks and then made their joint initial estimates. In addition, judges rated their confidence in the accuracy of their judgments. Once participants had provided initial estimates for all fifteen judgments tasks, they were asked to write down their initial estimates a second time on a separate sheet of paper, which would then be given to another individual or dyad as advice. In exchange, they then received a similar sheet of paper from their advisor and subsequently provided their final estimates, again accompanied by confidence ratings. Upon completion of the final estimates, participants were debriefed, thanked, and paid according to their performance.

2.1.3 Measures

Advice taking

We used the Advice Taking coefficient (AT, Harvey & Fischer, 1997), which is defined as (final estimate−initial estimate)/(advice−initial estimate). The AT equals the percent weight of advice when making the final estimate. In line with previous research, including the original study, we winsorized the AT scores at 0 and 1 (e.g., Gino et al, 2012; Minson & Mueller, 2012; Schultze, Rakotoarisoa & Schulz-Hardt, 2015; Soll & Larrick, 2009). Overall, we winsorized 2% of the AT scores in Study 1, 1.4% in Study 2, and 1.1% in Study 3 because of AT values greater than 1. In addition, we winsorized another 3.2% of the AT scores in Study 1, 2.5% in Study 2, and 1.7% in Study 3 because of AT scores smaller than 0, respectively. In 5.6%, 4.3%, and 4.5% of the trials, respectively, the AT score was not defined, because the advice equaled the initial estimate. Accordingly, we omitted these trials when computing the mean AT scores.

Confidence

Similar to the original study by Minson and Mueller (2012), we measured judges’ confidence by having them rate how confident they felt that their estimate did not deviate from the true values by more than ten percentage points (in case of the original tasks) or ten percent (in case of the new unbounded tasks). Participants provided the confidence ratings using 5-point Likert scales (1 = “not at all confident“, 5 = “very confident“). As in the original study, dyad members provided separate confidence ratings for each task, and we averaged them to obtain a measure of the dyad’s confidence. Ratings of initial confidence were missing for 6 trials in Study 1 (0.2%), and another 6 trials in Study 2 (0.3%), and final confidence ratings were missing in 18 (0.6%) and 17 trials (0.8%), respectively. There were no missing confidence ratings in Study 3. Trials with missing confidence ratings were omitted when computing mean initial confidence.

Accuracy

Due to the differences in scales between the original percentage estimates and the newly added unbounded judgment tasks, we used two different measures of accuracy. For the original tasks, we used the same measure as the original study, namely the mean absolute deviation (MAD) of the nine percentage estimates. In the new tasks, the MAD is not informative because it scales with the true value (i.e., a deviation from the true value of 1000 units is superb when estimating the population of a large city but marks an extreme error when judging the caloric value of 100 grams of vegetables). Therefore, we measured accuracy in the new tasks as the median absolute percent error (mdAPE) of the three respective estimates. Choosing the median rather than the mean limited the impact of extreme errors in single tasks. In order to allow for comparisons of accuracy between task types, we z-standardized the MAD and the two mdAPE scores.

2.2 Results

2.2.1 Preliminary analyses

We first investigated whether the three task types differed in the magnitude of judgment bias. As a standardized measure of bias, we computed the mean error for each of the fifteen tasks and divided it by the standard deviation of all estimates provided for that task. We then averaged the standardized biases by judgment task. The mean bias of the original tasks was 0.88 standard deviations as compared to a relatively low value of 0.14 standard deviations for the new tasks with low population bias, and 2.07 standard deviations for the new tasks with high population bias.

As another measure of bias, we investigated the bracketing rate (Soll & Larrick, 2009), which indicates how likely it is that two judgments will fall on opposite sides of the true value (a bracketing rate of 50% indicates full independence of judgments). A simulation with random pairings of initial estimates provided by individual judges yielded bracketing rates of 9% for the original tasks, 49% for the new tasks with low bias, and 1% for the new tasks with high bias. These descriptive results show that the manipulation of task type worked as intended.

2.2.2 Advice taking

We analyzed the AT scores in a 2 (judge type) × 2 (advisor type) × 3 (task type) mixed ANOVA with judge type and advisor type as between-subjects factors and task type as a within-subjects factor. The analysis revealed a pattern highly consistent with the original study. There was a main effect of judge type, F(1, 193) = 45.02, p < .001, η² = .11, whereas neither the main effect of advisor type nor the interaction of judge type and advisor type were statistically significant, F(1, 193) = 1.37, p = .242, η² = .00, and F(1, 193) = 0.29, p = .590, η² = .00, respectively. Task type had a significant effect on advice taking, F(2, 386) = 3.57, p = .029, η² = .01, but there were no significant interactions of task type with either judge type or advisor type, nor was there a significant three-way interaction, all Fs(2, 386) < 1.04, all ps > .357, all η² = .00.

Although, in line with our predictions, we did not find evidence of a moderating effect of task type, we also analyzed AT scores separately by task type. This separate analysis allows direct comparability of our replication to the original study. For the original percentage estimates, the 2 × 2 ANOVA revealed a main effect of judge type, F(1, 193) = 37.09, p < .001, η² = .16, due to individuals heeding advice more than dyads (M = 0.34, SD = 0.16 vs. M = 0.22, SD = 0.11). The main effect of advisor type was not significant, F(1, 193) = 2.61, p = .108, η² = .01, and neither was the interaction, F(1, 193) = 0.26, p = .610, η² = .00. In the new tasks with low population bias, we observed a similar pattern. Individuals weighted advice more than dyads (M = 0.40, SD = 0.27 vs. M = 0.23, SD = 0.19), F(1, 193) = 23.57, p < .001, η² = .11, but neither the main effect of advisor type nor the interaction were statistically significant, both Fs < 1. The same was true for the new tasks with high population bias. Mean AT scores were greater for individual judges than for dyads (M = 0.39, SD = 0.21 vs. M = 0.27, SD = 0.19), F(1, 193) = 17.32, p < .001, η² = .08, whereas the main effect of advisor type and the interaction both failed to reach statistical significance, both Fs < 1. These results are displayed in Figure 1.

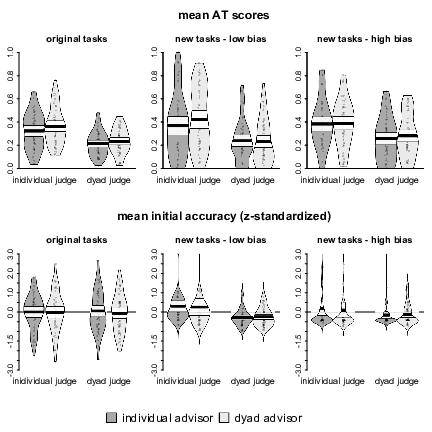
Figure 1: Pirate plots of mean AT scores and initial accuracy by judge type, advisor type, and judgment task. The plots show the distribution of the data as well as individual data points. The width of the beans corresponds to the estimated density. The bold horizontal lines represent the means, whereas the white bands denote 95% confidence intervals around those means. Beans for the accuracy plots were truncated at z- scores of 3.

As a final step, we tested the replicability of the finding that dyad judges heed the same advice by about two thirds the amount observed in individual judges’ advice taking. As noted above, this finding would support the idea that dyad judges understand how much the benefit of outside advice decreases when the judge is a dyad as compared to an individual. Collapsing across task types and advisor types, we first multiplied the mean AT scores of individuals by two thirds and treated the result as a point prediction for the dyad AT scores. We then tested the difference of dyad judges’ mean AT scores and the predicted AT score against zero using one-sample t-tests. If our predictions were accurate, we would expect a failure to reject the null hypothesis. Accordingly, we adjusted the α-level of the t-tests to .10 as suggested by Lakens (2017) and complemented the frequentist t-tests with a Bayesian analysis. Specifically, we computed Bayes Factors using the default Bayesian t-tests described by Rouder, Speckman, Sun, Morey and Iverson (2009). In this default test, the prior for the effect size d is a Cauchy distribution with the scaling factor equaling 0.707. The null hypothesis is defined as a point null hypothesis and, accordingly, the alternative hypothesis states that d is non- zero. As per convention, a Bayes factor greater than 3 indicates substantial evidence for the alternative hypothesis, a Bayes factor smaller than 1/3 provides evidence for the null hypothesis, and values in between are inconclusive (Jeffreys, 1961). We obtained a mean AT score of 0.36 for individual judges, resulting in a predicted AT of 0.24 for the dyads. The observed mean AT scores of the dyads was 0.23. Testing the deviation of the observed AT scores from the point prediction against zero yielded a non-significant result, t(102) = −0.63, p = .527, d = 0.06, BF = 0.13, and the Bayes factor indicated that the null hypothesis is about 7.5 times more likely to be true than the alternative given the data.

2.2.3 Initial confidence

A 2 (judge type) × 2 (advisor type) × 3 (task type) mixed ANOVA on judges’ mean initial confidence ratings revealed significant effects of judge type, F(1, 193) = 25.04, p < .001, η² = .07, task type, F(2, 386) = 43.47, p < .001, η² = .08, and their interaction, F(2, 386) = 5.51, p = .004, η² = .01. Advisor type had no significant effect on judges’ initial confidence, F(1, 193) = 3.50, p = .063, η² = .01, and neither did any of the remaining interactions, all Fs < 1.29.

Separate 2 × 2 ANOVAs on initial confidence showed that the interaction of judge type and task type was ordinal. For each of the three task types, dyad judges reported greater confidence than individual judges did. This difference was most pronounced in the new tasks with low bias (M = 2.87, SD = 0.63 vs. M = 2.32, SD = 0.82), F(1, 193) = 27.85, p < .001, η² = .13, somewhat weaker in the original tasks (M = 2.98, SD = 0.46 vs. M = 2.70, SD = 0.63), F(1, 193) = 12.82, p < .001, η² = .06, and weakest in the new tasks with high bias (M = 2.50, SD = 0.56 vs. M = 2.25, SD = 0.74), F(1, 193) = 7.37, p = .004, η² = .03.

2.2.4 Mediation analysis

Since we found qualitatively similar effects of judge type on advice taking and initial confidence in all three tasks, we tested the mediation across tasks using the lavaan package for R (Rosseel, 2012). A regression of mean AT scores on judge type showed a significant total effect, B = −.13, z = −7.04, p < .001. Regressing initial confidence on judge type also showed a significant effect, B = .33, z = 4.68, p < .001. When regressing mean AT scores on both judge type and initial confidence, judge type remained a significant predictor, B = −.11, z = −5.80, p < .001, but initial confidence was also related to AT scores, B = −.06, z = −3.38, p < .001. The indirect effect of -.02 was small but significant, as indicated by the 95% CI [-.034; -.006] excluding zero. Hence, the lower advice taking of dyads compared to individuals was partially mediated by dyads’ higher confidence ratings.

2.2.5 Initial accuracy

Since the error measures differed between task types due to the differences in response scales (bounded percentages vs. unbounded quantities), we first z-standardized the error measures by task type. We then subjected the z-standardized errors to a 2 × 2 × 3 ANOVA on the full design. The analysis revealed a main effect of judge type, F(1, 193) = 10.53, p = .001, η² = .02, which was qualified by an interaction of judge type and task type, F(1, 193) = 4.00, p = .019, η² = .01. No further effects were significant, all Fs < 1 (see Figure 1).

A 2 × 2 ANOVA of initial accuracy in the original tasks showed no significant effects, all Fs < 1. Dyad judges’ initial estimates were no more accurate than those of individual judges were (MAD: M = 15.81, SD = 4.00 vs. M = 15.83, SD = 3.83). In contrast, and in line with our predictions, there was a strong effect of judge type on initial accuracy in the new tasks with low bias, due to lower judgment errors of dyad judges (mdAPE: M = 31.83, SD = 19.94 vs. M = 55.80, SD = 57.03), F(1, 193) = 15.91, p < .001, η² = .07. Neither the effect of advisor type nor the interaction was significant, both Fs < 1. Contrary to what we expected, dyad judges also outperformed their individual counterparts in the new tasks with high bias, (mdAPE: M = 190.66, SD = 204.05 vs. M = 282.31, SD = 406.39), F(1, 193) = 4.09, p = .045, η² = .02. The remaining effects were not significant, both Fs < 1.

2.3 Discussion

First, the results of Study 1 show that the original findings of Minson and Mueller (2012) are replicable. Dyad judges heeded advice less, and they partially did so because they were more confident in their initial estimates. In line with our expectations, these effects seemed unaffected by task type. Even more importantly, we observed lower weights of advice both when dyad judges’ estimates were initially more accurate than their individual counterparts and when they were not. This result is consistent with the notion that groups act on a general belief that “two heads are better than one”, due to their inability to detect factors limiting the accuracy advantages of groups. Another finding that mirrored the original study of Minson and Mueller was that dyads’ weight of advice was about two thirds that of individual judges, which is in line with the idea that dyads have an accurate representation of the benefit of an additional opinion under the assumption of independent opinions. We also replicated the surprising finding that participants considered the number of judges but not the number of advisors when taking advice, that is, they did not weight advice given by dyads more strongly than advice given by individuals. Since the insufficient consideration of advisor type seems robust, on the one hand, but contradicts previous research showing that judges do consider the number of advisors (Mannes, 2009), on the other, this may warrant further research aiming to address the apparent inconsistency. The fact that dyad judges outperformed individuals in the tasks with high bias adds to recent research suggesting that group interaction can improve accuracy even in the light of substantial shared bias when tasks are unbounded (Minson et al., 2018; Stern, Schultze & Schulz-Hardt, 2017).

One potential limitation of Study 1 is that we manipulated the interdependence of dyad judgments indirectly via the content of the task rather than task structure. Despite our findings suggesting that this indirect manipulation worked as intended, there remains the possibility that the results we obtained are specific to such an exogenous manipulation. That is, the group process may have been comparable for all task types in the dyad judge conditions, but its detrimental effects on initial accuracy, such as those due to anchoring, may have varied depending on the task type. In particular, as Minson and Mueller (2013) noted, the estimates of dyads who enter discussion without making independent judgments, as was the case in the original study and our Study 1, do not actually reflect an integration of two independent estimates. Thus, it is conceivable that a more direct manipulation of interdependence of dyad judges via the task structure may yield different results. We address this possibility in Study 2.

3 Study 2

In Study 2, we manipulated the interdependence of dyad judges directly between subjects in addition to the within-subjects manipulation via population biases used in Study 1. To this end, we added another dyad condition, in which both members made independent judgments prior to discussion to ensure that the dyads’ initial estimates were composed of two independent judgments. Based on our hypothesis about the advice taking behavior of groups, we expected that dyads with and without independent pre-discussion judgments would differ in terms of initial accuracy but neither in terms of advice taking nor in terms of initial confidence.

3.1 Method

3.1.1 Participants and design

Participants were 250 university students. Similar to Study 1, we aimed for 50 individuals or dyads per cell. Participants were, on average, 24.19 years old (SD = 4.86); 143 were female (57%), and 104 were male (42%), 2 reported their gender as ‘other’ (1%), and one participant did not report any gender. Study 2 rests on a 3 (judge type: individual vs. dependent dyad vs. independent dyad) × 3 (task type: original vs. low bias vs. high bias) mixed design with judge type as a between-subjects factor and task type as a within-subjects factor.

3.1.2 Procedure

The procedure of Study 2 is identical to that of Study 1 with the following exceptions. First, we added a third judge type, namely independent dyads. Participants in this condition made independent individual estimates for all fifteen tasks prior to the group discussions, preventing interdependence stemming from anchoring effects. In all other regards, this condition was identical to the original dyad judge condition, which we now label as dependent dyads. Second, because advisor type had no reliable effects in the original study or in our replication, we dropped it as a factor, and all participants received advice from a single advisor. This meant that exchanging the initial estimates, as done in Study 1, was not feasible, because dyad judges would not have had recipients for their advice. Instead, we used the estimates of 50 randomly drawn individual judges from Study 1 as advice. Each advisor was randomly assigned to one individual judge, one dependent dyad, and one independent dyad, that is, judges in all three conditions received, on average, the exact same advice. Finally, we changed the incentive structure, because several participants in Study 1 remarked that they found large potential bonuses that diminished drastically over the course of the study very frustrating. Therefore, we offered a bonus of up to 3 Euros by adding 20 Cents for every final estimate that was “above average” in terms of accuracy. The benchmark for determining whether a judgment was above average in accuracy was the average accuracy of individual judges in Study 1.

3.2 Results

3.2.1 Advice taking

A 3 × 3 mixed ANOVA on the AT scores showed significant effects of judge type, F(2, 147) = 14.32, p < .001, η² = .09, and task type, F(2, 294) = 9.05, p < .001, η² = .03, but no significant interaction, F(2, 294) = 0.65, p = .628, η² = .004. Pairwise comparisons of the three judge types showed that, as in Study 1, dependent dyads heeded advice less than individuals (M = 0.21, SD = 0.12 vs. M = 0.31, SD = 0.14), t(94.97)¹ = −3.97, p < .001, d = 0.79. The same was true for the independent dyads (M = 0.19, SD = 0.11 vs. M = 0.31, SD = 0.14), t(92.67) = −4.88, p < .001, d = 0.87. As expected, there was no significant difference in AT scores between the two dyad conditions, t(97.60) = 0.90, p = .371, d = 0.19 (see Figure 2).

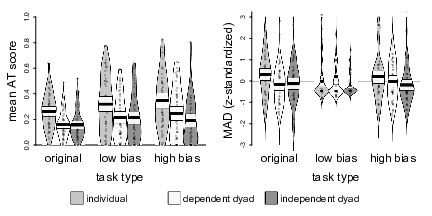
Figure 2: Pirate plots of mean AT scores and initial accuracy by judge type in Study 2. The plots show the distribution of the data as well as individual data points. The width of the beans corresponds to the estimated density. The bold horizontal lines represent the means, whereas the white bands denote 95% confidence intervals around those means. Beans for accuracy are truncated at z-scores of 3.

As in Study 1, we compared dyad judges’ mean AT scores to a point prediction derived from multiplying the average AT score of dyads by two thirds. In this analysis, we collapsed across task types and across dyad types (based on our initial reasoning, we would expect that dependent and independent dyads behave in the same fashion, and Study 2 showed no evidence suggesting otherwise). The observed level of individual judges’ advice taking was 0.29, leading to a predicted level of advice taking in dyads of 0.19. Dyad judges’ actual mean AT score was 0.18. Despite the more lenient α -level of .10 for this test, the difference between observed and predicted AT scores was not significant, t(99) = −1.18, p = .240, d = 0.12, BF = 0.22, with the Bayes Factor suggesting that the null hypothesis is 4.6 times more likely than the alternative hypothesis.

3.2.2 Initial confidence

Analogous to the AT scores, a 3 × 3 mixed ANOVA on judges’ initial confidence showed main effects of judge type, F(2, 147) = 5.37, p = .006, η² = .05, and task type, F(2, 294) = 54.89, p < .001, η² = .11, but no significant interaction, F(2, 294) = 1.39, p = .236, η² = .01. The main effect of task type was due to notably lower confidence when working on the unbounded tasks with high bias as compared to the original tasks or the unbounded tasks with low bias (M = 2.40, SD = 0.66 vs. M = 2.94, SD = 0.57 vs. M = 2.70, SD = 0.70), all ts > 3.78, all ps < .001, all ds > .30. Pairwise comparisons of judge types revealed the expected result. Dependent dyad judges were more confident than individuals (M = 2.77, SD = 0.56 vs. M = 2.50, SD = 0.50), t(96.43) = 2.58, p = .011, d = 0.52. This was also the case for the independent dyads (M = 2.80, SD = 0.48 vs. M = 2.50, SD = 0.50), t(97.88) = 3.14, p = .002, d = 0.62. In line with our expectations, the two dyad conditions did not differ in initial confidence, t(95.47) = −0.31, p = .758, d = 0.07.

3.2.3 Mediation analysis

We tested the mediating role of initial confidence collapsing across the two dyad conditions since they showed very similar levels of advice taking and confidence. Similarly, we averaged across the three task types because task type did not moderate the effects of judge type for either advice taking or initial confidence. A regression of mean AT scores on a dummy variable, coding judge type as either individual or dyad, showed a significant effect, B = −.11, z = −5.33, p < .001. Regressing initial confidence on the dummy variable also showed a significant effect, B = .29, z = 3.29, p < .001. When regressing mean AT scores on both judge type and initial confidence, judge type was still a significant predictor, B = −.11, z = -5.00, p < .001, but initial confidence was not, B = −.01, z = −0.59, p = .553. Thus, we were unable to replicate the mediation effect from the original study and our Study 1, also indicated by a non-significant indirect effect of -.003, 95% CI [-.02; .01].

3.2.4 Initial accuracy

As in Study 1, we used z-standardized errors as the dependent variable to ensure comparability between task types. Contrary to our expectations, a 3 × 3 mixed ANOVA showed only an effect of judge type, F(2, 147) = 3.79, p = .025, η² = .02. The interaction of judge type and task type, which we observed in Study 1, was not significant, F(2, 294) = 1.59, p = .177, η² = .01. Due to the standardization of errors within tasks, a main effect of task type was impossible, F ≈ 0. Pairwise comparisons of judge types showed that independent dyads were initially more accurate than individual judges, as indicated by smaller standardized errors (M = −0.17, SD = 0.84 vs. M = 0.17, SD = 1.02), t(91.21) = 3.01, p = .003, d = 0.53. The dependent dyads were descriptively more accurate than the individual judges (M = 0.00, SD = 1.09 vs. M = 0.17, SD = 1.02) and less accurate than the independent dyads (M = 0.00, SD = 1.09 vs. M = −0.17, SD = 0.84). Descriptively, this pattern is in line with our expectations, but both differences failed to reach statistical significance, both ts < 1.46, both ps > .157, both ds < 0.37.

Although task type did not emerge as a moderator of judge type effects in the analyses of initial accuracy, we analyzed initial accuracy in the original tasks for comparability with Study 1 and the original study. Initial accuracy differed significantly as a function of judge type, F(2, 147) = 3.63, p = .029, η² = .05. Pairwise comparisons showed that, in line with our expectations, independent dyads outperformed individual judges in terms of initial accuracy (MAD: M = 15.34, SD = 4.00 vs. M = 17.08, SD = 3.99), t(98.00) = 2.19, p = .031, d = 0.44. In contrast to the original findings and our Study 1, dependent dyads, too, were more accurate than individuals (MAD: M = 15.18, SD = 3.79 vs. M = 17.08, SD = 3.99), t(97.74) = 2.45, p = .016, d = 0.49, and the two dyad conditions did not differ significantly (MAD: M = 15.34, SD = 4.00 vs. M = 15.18, SD = 3.79), t(97.71) = −0.20, p = .842, d = 0.04.

3.3 Discussion

The results of Study 2 again replicate lower weights of advice in dyads relative to individual judges, weight of advice in dyads consistent with the idea that dyad judges understand how much the added value of an outside opinion diminishes when the initial estimate is based on two independent opinions, and greater confidence of dyads in their initial confidence (although we were unable to replicate the mediation effect of confidence). However, the unexpected results of our analysis of judges’ initial accuracy make it difficult to interpret the results regarding our hypothesis that groups heed advice less irrespective of whether their greater initial accuracy warrants it. The finding that dependent dyads were in between individuals and independent dyads in terms of accuracy fits Minson and Mueller’s (2012, 2013) notion that immediate discussion may hinder groups’ accuracy by inducing anchoring effects. However, since the difference in accuracy between dependent dyads and independent dyads, as well as the difference between dependent dyads and individuals, failed to reach statistical significance, we cannot draw firm conclusions about dyads’ insensitivity to their initial accuracy when deciding how to weight advice. Limiting the analysis to the original judgment tasks by Minson and Mueller (2012) does not solve the problem either. In contrast to our first study, and in contrast to Minson and Mueller’s original results, dependent dyads significantly outperformed individuals in terms of initial accuracy and even matched the initial accuracy of independent dyads. Arguably, the surprisingly good performance of dependent dyads, particularly in the original tasks, might have been a chance finding. To clarify this issue, we conducted a third study.

4 Study 3

Study 3 is a slightly modified replication of Study 2. So far, we focused on situations in which dyad judges’ initial accuracy fell short of the accuracy of an aggregation of independent opinions. That is, we compared situations in which reduced weights of advice were justified (due to independence of dyad judges’ individual opinions) with situations in which dyad judges’ weight of advice should have been higher because this independence was lacking. In Study 3, we aimed to expand our focus to the opposite situation, characterized by dyad judges’ initial estimates being even more accurate than a simple aggregation of two independent judgments (i.e., dyads achieving synergy due to effective group processes). This allowed us to explore whether groups’ inability to detect insufficient performance due to interdependence of opinions is mirrored by a corresponding inability to detect superior performance due to synergy. To this end, we replaced the unbounded judgment tasks used in the previous studies with a new set of tasks showing a high probability of extreme errors. We included these tasks because previous research has found that dyads working on unbounded tasks with independent pre-discussion estimates can outperform the average of two independent judgments specifically by correcting extreme errors (Minson et al., 2018; Stern et al., 2017).

4.1 Method

4.1.1 Participants and design

As in Study 2, participants were 250 university students (50 individuals or dyads per cell). They were, on average, 23.63 years old (SD = 3.87); 146 were female (59%), 101 were male (41%), and 4 participants did not report any gender. The design of Study 3 was a 3 (judge type: individual vs. dependent dyad vs. independent dyad) × 2 (task type: original vs. unbounded) design with judge type as a between-subjects factor and task type as a within-subjects factor.

4.1.2 Procedure

The procedure of Study 3 is identical to that of Study 2 with the following exceptions. First, we replaced the six unbounded tasks with low and high population bias with nine unbounded judgment tasks based on the results of a pretest. We selected the new tasks because, while most participants were well calibrated, a minority made large judgment errors, that is, their errors differed from the average error by at least one order of magnitude. Examples for the new tasks are estimating the diameter of the earth or the speed of sound in air. As in the previous studies, we used the mdAPE as the error measure for the new unbounded tasks. Second, we changed the incentive structure back to a subtractive mode but in a somewhat less severe, and arguably less frustrating, fashion than in Study 1 to account for the possibility that changes in the incentive structure may have influenced the performance of interdependent dyads in Study 2. Participants could receive a bonus of up to 9 Euro in addition to their participation fee. For each task in which their final estimate deviated more than 10 percentage points (or ten percent for the unbounded tasks) from the true value, their bonus was reduced by 50 Cents. This incentive structure ensured that participants did not lose their whole bonus because of one extreme error, which seemed particularly appropriate given how we chose the new unbounded tasks. Finally, except for independent dyad members’ individual pre-discussion judgments, Study 3 was computer-based with dyad judges working together on one computer.

4.2 Results

4.2.1 Advice taking

A 3 × 2 mixed ANOVA on the AT scores showed a significant main effect of judge type, F(2, 147) = 7.46, p < .001, η² = .07, and a significant main effect of task type, F(1, 147) = 7.46, p = .008, η² = .02, but no significant interaction, F(2, 147) = 1.49, p = .227, η² = .01. The effect of task type was due to somewhat higher weights of advice in the new unbounded tasks compared to the original percentage estimates (M = 0.27, SD = 0.18 vs. M = 0.23, SD = 0.14). Pairwise comparisons of judge types showed the familiar pattern: Dependent dyads heeded advice less than individuals (M = 0.23, SD = 0.10 vs. M = 0.30, SD = 0.16), t(84.46) = 2.89, p = .004, d = 0.58, as did independent dyads (M = 0.21, SD = 0.12 vs. M = 0.30, SD = 0.16), t(89.56) = 3.32, p = .001, d = 0.81. AT scores did not differ significantly between the two dyad conditions, t(96.9) = 0.68, p = .500, d = 0.13 (see Figure 3). These results also hold when analyzing the two task types separately, all ts > 2.25, ps < .027, ds > 0.44 for comparisons of dyads vs. individual judges, and both ts < 1.28, ps > .206, ds < 0.26 for the comparisons of the two dyad types.

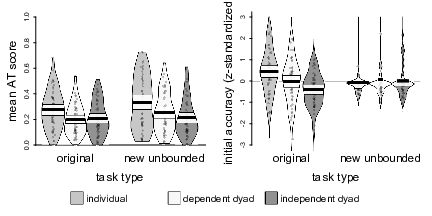
Figure 3: Pirate plots of mean AT scores and initial accuracy by judge type and task type in Study 3. The plots show the distribution of the data as well as individual data points. The width of the beans corresponds to the estimated density. The bold horizontal lines represent the means, whereas the white bands denote 95% confidence intervals around those means. Accuracy is z-standardized for comparability between the two task types. Beans for the accuracy plots were truncated at z- scores of 3.

As in the previous studies, we concluded the analysis of AT scores by comparing dyad judges’ AT scores to two thirds of the average weight individual judges assigned to the advice. Similar to Study 2, we collapsed across task types and dyad types in this analysis, and we again set the α -level to .10. The mean of the individual AT scores was 0.31, yielding a predicted AT score of 0.20 for the dyads as compared to their actual mean AT of 0.22. Once more, the difference between observed and predicted levels of advice taking in dyads was non-significant, t(99) = 1.52, p = 0.131, d = 0.15, BF = 0.34, and the Bayes factor favors the null hypothesis, suggesting that it is three times more likely to be true than the alternative hypothesis.

4.2.2 Initial confidence

A 3 × 2 mixed ANOVA on judges’ initial confidence revealed significant main effects of judge type, F(2, 147) = 4.08, p = .019, η² = .04, and task type, F(2, 147) = 137.54, p < .001, η² = .14, but no significant interaction, F(2, 147) = 1.07, p = .345, η² = .003. The main effect of task type resulted from participants’ greater initial confidence when working on the original tasks compared to the new unbounded tasks (M = 2.91, SD = 0.67 vs. M = 2.39, SD = 0.66). Pairwise comparisons of judge types showed that dependent dyads were more confident than individual judges (M = 2.74, SD = 0.59 vs. M = 2.45, SD = 0.71), t(94.79) = −2.20, p = .030, d = 0.44, and so were the independent dyads (M = 2.75, SD = 0.44 vs. M = 2.45, SD = 0.71), t(81.41) = −2.51, p = .014, d = 0.69. Initial confidence did not differ significantly between dyad types (M = 2.74, SD = 0.59 vs. M = 2.75, SD = 0.44), t(90.32) = −0.07, p = .941, d = 0.02. These results replicate those of Study 1 and the original study.

4.2.3 Mediation analysis

We tested the mediating role of initial confidence collapsing across the two dyad conditions since they showed very similar levels of advice taking and confidence. We also collapsed across task types because task type neither interacted with judge type in the analysis of advice taking nor in the analysis of initial confidence. A regression of mean AT scores on a dummy variable, coding judge type as either individual or dyad, showed a significant effect, B = −.09, p < .001. Regressing initial confidence on the dummy variable also showed a significant effect, B = .29, p = .004. When regressing mean AT scores on both the judge type dummy and initial confidence, both were significant predictors, B = −.08, p < .001, and B = .04, p = .045, respectively. The indirect effect, although in the predicted direction, was rather small at −.01 and failed to reach statistical significance, 95% CI [−.023; .002]. Thus, as in Study 2, we failed to replicate the mediating role of initial confidence.

4.2.4 Initial accuracy

As in the previous studies, we z-standardized initial accuracy within task types. We then analyzed the standardized errors in a 3 × 2 mixed ANOVA, finding a main effect of judge type, F(2, 147) = 4.00, p = .020, η² = .02, which was qualified by an interaction of judge type and task type, F(2, 147) = 5.58, p = .005, η² = .04. As in Study 2, z-standardization within tasks meant that it was not possible to find an effect of task type in the analysis, F ≈ 0.

To disentangle the interaction effect, we ran two separate one-factorial ANOVAs on initial accuracy. For the original tasks, initial accuracy differed significantly by judge type, F(2, 147) = 10.01, p < .001, η² = .12. Pairwise comparisons showed that, as in Study 2, independent dyads were initially more accurate than individual judges (MAD: M = 13.05, SD = 2.51 vs. M = 15.82, SD = 3.33), t(91.01) = −4.69, p < .001, d = 1.11. Also as in Study 2, dependent dyads were in between the other two conditions in terms of accuracy. However, this time, their initial accuracy advantage over individuals was significant (MAD: M = 14.28, SD = 3.37 vs. M = 15.82, SD = 3.33), t(97.98) = −2.29, p = .024, d = 0.46. The same was true for the difference between dependent and independent dyads (MAD: M = 13.05, SD = 2.51 vs. M = 14.28, SD = 3.37), t(90.45) = −2.07, p = .041, d = 0.50.

For the unbounded tasks, the results were contrary to our expectations. Instead of particularly pronounced differences in accuracy between individual and dyad judges, the ANOVA showed virtually no differences in accuracy between judge types, F(2, 147) = 0.19, p = .828, η² = .003.

4.3 Discussion

The results of Study 3 further support the robustness of less advice taking and greater confidence in dyads relative to individual judges, although we, similar to Study 2, failed to replicate the mediation of reduced advice taking in dyads via their increased confidence (descriptively, the indirect effect was in the expected direction). As in the previous studies, dyads’ weight of the advice was about two thirds that of the individual judges. The analyses of initial accuracy were partly consistent with our expectations. The lack of accuracy differences between judge types in the unbounded tasks with extreme errors was surprising in the light of previous research (Minson et al., 2018), and it denied us the opportunity to compare advice taking between dyads and individuals in situations where dyads perform better initially than a mere aggregate of individuals estimates would suggest. However, making a virtue of necessity, we can use the absence of accuracy differences in the unbounded tasks to draw additional conclusions about our hypothesis that lower weights of advice in dyads occur irrespective of whether they are reflected in greater (vs. similar) initial accuracy when compared to individuals. As in Study 1, task type moderated differences in initial accuracy but not differences in advice taking.

Most importantly, Study 3 allowed us to conduct the experimental test of our hypothesis that was not possible in Study 2 due to the lack of accuracy differences between dependent and independent dyads. The analyses of initial accuracy in the original tasks showed that discussing the tasks without making independent pre-discussion estimates can hinder dyads’ performance, arguably due to numerical anchoring. On the other hand, they suggest that dyads seem to be unaware of the detrimental effects because their level of advice taking matched that of the initially more accurate independent dyads.

5 Meta-analysis

While the analyses of advice taking and initial confidence yielded similar results in all three studies, some findings were somewhat inconsistent between studies. This concerns primarily the mediation analyses and the analyses of initial accuracy in the original Minson and Mueller (2012) tasks. Therefore, we analyzed these effects across all three studies in a meta-analysis. We started the analyses by investigating the mediation of lower weights of advice in dyads via greater initial confidence. Similar to the analyses of the individual studies, we collapsed across the two advisor type conditions in Study 1 and across task types in all three studies. We also collapsed across the two dyad types in Studies 2 and 3. We then subjected the combined data set to a mediation analysis comparable to those reported in the individual studies. Since the effects of judge type on advice taking and initial confidence may vary between studies, we first assessed the necessity to model possible dependencies in the data. To this end, we compared a multi-level model predicting mean AT scores from judge type (dummy coded, 0 = individual, 1 = dyad) with a regular regression model treating judges from all three studies as independent observations. We use the R packages lmer (Bates, Maechler, Bolker & Walker, 2015) and lmerTest (Kuznetsova, Brockhoff & Christensen, 2017) to run the multi-level analyses. The multi-level model contained random intercepts as well as random slopes for judge type. A likelihood ratio test comparing the two models revealed that the multi-level provided a significantly better fit to the data than the regular regression model, χ²(3) = 12.40, p = .006. Thus, we ran the meta-analysis of the mediation using multi-level models. The effect of judge type on mean AT scores in the multi-level model reported above was significant, B = −0.11, t(8.83) = −8.62, p < .001.² A similar random slopes model predicting judges’ mean initial confidence also yielded a significant effect of judge type, B = 0.29, t(128.31) = 6.01, p < .001. When predicting mean AT scores from both judge type and mean initial confidence in a multi-level model with random intercepts and random slopes for judge type as well as for man initial confidence, judge type sill predicted advice taking, although the size of the effect was slightly reduced, B = −0.10, t(34.21) = −8.24, p < .001. Mean initial confidence, while having an effect in the expected direction, was no significantly related to advice taking, B = −0.03, t(2.16) = −1.91, p = .186. We tested for mediation using the mediate function of the mediation package (Tingley, Yamamoto, Hirose, Keele & Imai, 2014). The indirect effect was -0.01, which amounts to 10% of the total effect of judge type on advice taking. This indirect effect was statistically significant as the bias-corrected and accelerated 95% CI based on 10,000 bootstrap samples excluded zero [-0.02295; -0.00003]. Omitting the random slopes of mean initial confidence in the test of the indirect effect yields qualitatively similar results. The same is true, when restricting this analysis to the original judgment tasks. Thus, although we failed to replicate the mediation effect reported in the original study in two of our three studies, our aggregated data speaks to its replicability.

Next, we analyzed judges’ initial accuracy in the original Minson and Mueller (2012) percentage estimates. Again, we first assessed the necessity to model possible dependencies in the data by comparing a multi-level model predicting initial accuracy from judge type (individual vs. dependent dyad vs. independent dyad) with a regular regression model treating judges from all three studies as independent observations (remember that all dyads from Study 1 were dependent dyads). The multilevel model, which contained random intercepts and random slopes for judge type, did not provide a significantly better fit to the data than the regular regression model, χ²(6) = 7.61, p = .268. We thus proceeded to analyze initial accuracy in a one-factorial ANOVA with judge type as a between-subjects factor, finding significant differences, F(2, 494) = 9.14, p < .001, η² = .04. Pairwise comparisons showed that the initial estimates of independent dyads were more accurate than those of the individual judges (M = 14.19, SD = 3.51 vs. M = 16.15, SD = 3.77), t(212.98) = 4.41, p < .001, d = 0.53. The same was true, albeit to a lesser degree, for the estimates of dependent dyads (M = 15.28, SD = 3.84 vs. M = 16.15, SD = 3.77), t(394.69) = 2.27, p = .024, d = 0.23. However, the accuracy of dependent dyads fell short of that of their independent counterparts (M = 15.28, SD = 3.84 vs. M = 14.19, SD = 3.51), t(213.46) = −2.46, p = .015, d = 0.29. These results once again support Minson and Mueller’s (2012) argument that immediate discussion can hinder group performance in quantity estimation. Likewise, it supports our hypothesis that dyads fail to take the possible interdependence of their members into account when heeding advice, as differences in accuracy between judge types were not reflected in comparable differences in advice taking.

Our final analysis concerned the idea that dyads heed the same advice about two thirds as much as individuals do. We subjected the three tests comparing dyad judges’ mean AT scores to the point predictions derived by multiplying individual judges mean AT scores by two thirds to a random effects meta-analysis. Specifically, we tested the deviations from the model predictions against zero in an intercept only multi-level model with a random intercepts for experiment using the lmerTest package. The meta-analytic estimate of the deviation from the point predictions was -0.0004, 90% CI [-0.012; 0.011], suggesting that, on average, the point prediction provided a very good description of dyad judges’ behavior (see also Figure 4). Note that a similar analysis based on the individual trials yields a qualitatively equivalent pattern of results. Specifically, we predicted the deviation of dyads’ AT scores from the point predictions in an intercept only multi-level model with random intercepts for judgment task nested within judges who were nested within experiments. The fixed intercept was not significantly different from zero, B = 0.00004, t(4330) = 0.01, p = .996, 90% CI [-0.011; 0.011].

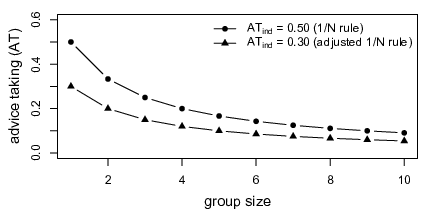
Figure 4: Results of the meta-analysis testing the fit of the point predictions of advice taking in dyads. The points represent the deviation of observed AT sores from the prediction. Error bars correspond to the 90% CIs reported on the right-hand side. The width of the diamond representing the meta-analytic random effects estimate also corresponds to the respective 90% CI displayed on the right.

6 General discussion

In three studies, we investigated how dyads as compared to individuals use advice in quantitative judgment tasks. Our first aim was to test whether the core findings of the, so far, only published study on advice taking in groups (Minson & Mueller, 2012) are replicable. The results of our analyses suggest that they are, both because they emerged consistently in all three of our studies and, in the cases where results were inconsistent between studies, the meta-analysis revealed them. Specifically, our results show that dyad judges consistently heed the same advice less than individual judges, and this effect is partially mediated by dyads’ greater confidence in the accuracy of their pre-advice judgments. Note, however, that the indirect effect of judge type on advice taking was rather small, suggesting that there may be additional mediating variables at work.

Second, and more importantly, we aimed to solve the debate about the appropriateness of dyad judges’ greater resistance to advice that inspired the present research. This solution entailed shifting the focus from whether dyads heeding advice less than individuals is appropriate to why they do so. Accordingly, we tested the hypothesis that groups heed advice less than individuals, irrespective of whether this behavior is justified by greater initial accuracy. Our results are fully consistent with this hypothesis. We found that dyads weighted advice less than individuals did in all three studies, irrespective of task content. That is, dyad judges heeded advice less both in tasks where they performed better than individuals did initially and in tasks where they did not. In addition, dyads whose members immediately began discussing the tasks performed worse initially, on average, than dyads whose members made independent pre-discussion judgments. Again, these differences in initial accuracy did not go along with differences in advice taking between the two dyad types. This dissociation between dyad judges’ initial accuracy and their advice taking behavior, both within dyads and between dyad types, suggests that groups act on the general premise that ‘two heads are better than one’, and that they fail to recognize when this is not the case. These results make perfect sense if we consider that the factors that likely impeded dyad judges’ initial accuracy in our studies, namely shared biases and anchoring effects, are difficult to correct for because they usually escape conscious awareness.

Despite our focus on explaining why dyads heed advice less than individuals, we can still make some concluding statements about the appropriateness of this behavior. While we argued that dyads should heed advice as if their members had contributed independently to the joint initial estimates (Schultze et al., 2013), Minson and Mueller (2013) responded that they should heed advice as much as individuals (or fully dependent dyads). Our meta-analysis of initial accuracy tells us that, as is often the case, the truth lies in between. Dependent dyads made more accurate individual judgments than individuals did, but their accuracy fell short of the accuracy of independent dyads. Therefore, dependent dyads should heed advice somewhat less than individuals, but still to a larger extent than independent dyads.

6.1 Deriving a model of advice taking in groups

Our data not only support the hypothesis that dyads heed advice less than individuals do because they believe that two heads are better than one. It is also consistent with the idea that dyads know how much better two heads are given the independence of all opinions involved and that this knowledge is reflected in their advice taking behavior. Our reasoning here was as follows: if all people involved in a JAS contribute an independent opinion, dyads should heed the advice of an advisor two thirds as much as individual judges should, ceteris paribus, and assuming that the well-known tendency to underweight advice would persist unchanged in the dyad context. When inspecting the mean levels of advice taking, this is exactly what we found. Making point predictions about the expected level of advice taking in dyads allowed us to define our predictions as the null hypothesis in the respective tests. In all three studies, we failed to reject the null hypothesis, and the complementing Bayesian analyses showed evidence in favor of the null hypothesis. The accuracy of our predictions became particularly apparent in a meta-analysis. The difference of the predicted weight of advice, based on the mean AT scores of 194 individual judges, deviated from the mean of, in total, 303 dyad AT scores by only 0.0004 points. (i.e., less than a tenth of a percentage point). Thus, is seems that we can predict dyad judges’ behavior quite accurately – at least on an aggregate level – from a few simple assumptions if we know how individual judges use the same advice.

Although we were concerned only with dyadic advice taking, we can nonetheless make use of the observed pattern to formulate a generalized predictive model of advice taking in groups. The only additional assumption is that the processes we believe to operate in dyad judges (understanding the added value of additional information, neglect of possible interdependence within the group, and group members’ individual resistance to advice) work in the same fashion in groups of any size. The expected weight of advice for a specific group size is then given by:

(1)

Here, AT _N is the expected weight of advice assigned to a single advisor when the judge is a group of size N, and AT _ind is an estimate of how strongly individual judges weight the same advice. The second factor of the right side, AT _ind divided by 0.50, is an individual egocentric discounting factor, that is, it indicates the ratio of individual judges’ actual weight of advice as compared to the normatively correct weight of advice assuming equal expertise. As shown in Figure 5, in cases where individual judges do not egocentrically discount advice (AT _ind equals 0.50), the model prediction represents equal weighting of all opinions, also known as the 1/N rule. If individual judges discount advice, the prediction represents a downward projection of the 1/N curve so that the ratio of the 1/N rule and the adjusted 1/N rule remains constant and equals the individual egocentric advice discounting factor, AT _ind divided by 0.50 (see Figure 5).

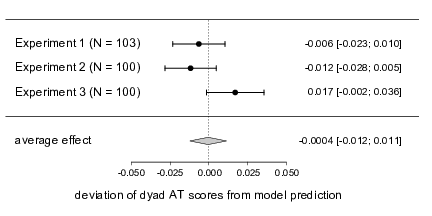
Figure 5: Point predictions of the weight of advice (AT) placed on the judgment of a single advisor as a function of group size and level of advice taking observed in individual judges. The upper line reflects the expected weight of advice when individual judges do not egocentrically discount advice. The lower line shows the model prediction for a hypothetical case in which individual judges weight advice from an individual advisor by 30% (egocentric advice discounting factor of 0.60).

Of course, one can contest the idea that we can generalize from the behavior of dyads to that of larger groups. Groups with three and more members can differ qualitatively from dyads, for example, because the former allow for majority-minority constellations (for a debate on this issue, see, Moreland, 2010; Williams, 2010). A comprehensive test of our model of advice taking is beyond the scope of the studies reported here. Despite the repeated failure to reject the model predictions in our dyadic settings, additional research is required to expand the test of the model to larger groups. Ideally, future studies should vary the size of the groups receiving advice to provide a more comprehensive test of the adjusted 1/N rule’s predictive power.

6.2 Limitations and direction for future research

We can think of at least three limitations that need consideration. First, as is standard in research on advice taking, judges in our studies did not interact with their advisors. Thus, it remains unclear to what extent our findings hold in situations, in which judges can ask their advisors to elaborate on their recommendations and scrutinize the advisor’s justifications. It is conceivable that dyads may be more effective at determining the quality of advice when given the chance to interact with their advisor, for example, because they can come up with more diagnostic questions about the quality of the advice. Accordingly, future research could investigate whether dyads – or groups, in general – may handle advice more effectively in more socially rich contexts.

Second, our analyses of advice taking in dyads are restricted to the average behavior of the average dyad. We know from previous research (Soll & Larrick, 2009; Soll & Mannes, 2011) that average AT scores do not necessarily correspond to judges’ trial-by-trial behavior. In other words, our ideas about how dyads use advice might accurately describe the average behavior of dyads (and even that of larger groups) without accurately capturing any particular dyad’s responses on any particular trial. A related question is whether we would be able to make accurate predictions about the average behavior of a specific dyad given sufficient knowledge about the individual advice taking behavior of its members. Such a prediction might be possible if we know about the idiosyncratic levels of advice resistance that the dyad’s members display outside the group context. The mean of dyad members’ individual AT scores could serve as the input for a respective model, resulting in a point prediction for that dyad’s future advice taking.

Finally, when testing the idea that dyads understand how the value of an outside opinion decreases with the number of independent opinions already contained in the joint initial estimate, we compared dyads’ average behavior to fixed-value predictions. However, since these predictions are derived from individual judges’ behavior, they are prone to random variation and measurement errors. Treating the model predictions as fixed values increases the chance of rejecting the null hypothesis. On the one hand, this means subjecting the model to a more conservative test. However, it also bears the risk of rejecting the model prematurely whenever individual judges’ behavior is relatively extreme due to sampling error.

6.3 Conclusion

Integrating our own perspective on how groups should handle advice with the conflicting opinions of Minson and Mueller (2012, 2013), we were able to derive and test an explanation as to why groups heed advice less than individuals. Besides showing the importance of constructive scientific debates for the advancement of our field, our findings pave the ground for future research aiming to understand and improve advice taking in dyads – and ultimately groups, in general. Central to this enterprise is the finding that insufficient weights of advice in dyads do not reflect greater resistance to advice but rather originate in dyads’ neglect of interdependence. Hence, a promising step in making dyads, or groups, better advisees could consist of applying techniques known to ameliorate shared biases and anchoring effects such as devil’s advocacy. If such group-specific interventions prove effective, then groups may very well outshine individuals when trying to make the best use of advice.