1 Introduction
1.1 The gambler’s fallacy
The gambler’s fallacy involves the mistaken belief that for a series of random binary alternatives, runs of a particular outcome will be balanced by a tendency for the opposite outcome. This widely known fallacy is observed in many situations in everyday life (e.g., when tossing a coin), although gambling in casinos is the canonical domain of its occurrence. This error of judgment was first documented by Laplace (1796/Reference Laplace, Truscott and Emory1951), which numerous studies in probability learning afterwards have empirically confirmed its reality in laboratory settings (e.g., Derks, Reference Derks1962, Reference Derks1963; Edwards, Reference Edwards1961; Jarvik, Reference Jarvik1951; Witte, Reference Witte1964). More recent studies reported that, when subjects are asked to generate or recognize random sequences in experimental tasks, their responses typically show a negative recency effect, reflecting a bias against repeating the same choice (see, e.g., Bar-Hillel & Wagenaar, Reference Bar-Hillel and Wagenaar1991). For example, participants in Clotfelter and Cook’s (Reference Clotfelter and Cook1993) lottery game displayed behavior consistent with the gambler’s fallacy, while betting on the outcome of the drawing of a three-digit number. The study showed that players bet significantly less money on recently drawn numbers, and that bets placed on such numbers gradually returned to previous amounts in the course of time.
Within the study of the faulty judgments about randomness, research has demonstrated that even explicitly teaching individuals about the nature of chance events has not proved to be sufficient in reducing or eliminating the bias (Beach & Swensson, Reference Beach and Swensson1967), unless people are trained to perceive each future event as if it is not being part of a longer sequence. In this case, they consider every event as independent with no relation to past outcomes (Roney & Trick, Reference Roney and Trick2003).
Why (and under which circumstances) do people believe the successive outcomes of a purely random process to be negatively autocorrelated? Perruchet, Cleermans and Destrebecqz (Reference Perruchet, Cleeremans and Destrebecqz2006) suggested that conscious expectancy about the likely pattern of events might be responsible for observations of the gambler’s fallacy. These authors have demonstrated in laboratory experiments that when two unrelated events E1 and E2 are repeatedly displayed in close temporal succession, people’s expectancy for E2 is highest after a long run of “E1 alone” events and lowest after a long run of E1–E2 pairings, consistent with the gambler’s fallacy effect. Further, this difference in degree of expectation increases as a function of the length of the preceding run.
Kahneman and Tversky (Reference Burns and Corpus1972) explanation of the gambler’s fallacy attributed the phenomenon to a general misconception of the laws of chance, which is associated with the operation of the representativeness heuristic. They argued that people commonly believe that small samples must be representative of the larger population (Tversky & Kahneman, Reference Derks1971, Reference Tversky and Kahneman1974), and thus erroneously expect streaks to eventually even out in order to be representative of their generating process. Consequently, people expect sequences exemplifying chance process to contain many more alternations than would actually be produced by a random process. For example, people typically tend to view a random sequence of coin tosses as having nearly equal distribution of heads and tails in any short segment of the sequence, and thus attach higher probability to roughly equal sequences than the correct probability. Similarly, after observing a long run of red on the roulette wheel, most people predict that black would show up next.
Another possible explanation of the gambler’s fallacy suggests that, while sampling a finite set of outcomes without replacement, observing a particular outcome lowers the chances of observing that outcome the next time. Consequently, it makes sense to expect negative recency (i.e., a tendency to predict the opposite of the last event). In two experiments, Ayton and Fischer (Reference Ayton and Fischer2004) empirically demonstrated negative recency in subjects’ expectations about random binary outcomes from a roulette game. They concluded that the gambler’s fallacy results from the experience of negative recency in sequences of natural events (as opposed to human skilled performance), similar to sampling without replacement. Further, Burns and Corpus (Reference Burns and Corpus2004) found that a tendency not to follow streaks exists when people judge the underlying process generating the events to be random (e.g., machines), more than when the generating mechanism is thought to be non-random (e.g., humans). Thus, in contexts involving unintentional agents, such as spins of a roulette wheel, streaks represent random accidents that are unlikely to continue (Caruso & Epley, Reference Caruso and Epley2004).
1.2 Soccer penalty kick shootouts
Penalty shootouts in soccer are relatively rare. Games that end with a tie, a common result, are generally recorded as a tie in soccer leagues worldwide. However, in certain stages of various tournaments, including the FIFA World Cup and UEFA Euro Cup, a winner must be determined. If the game is tied after 90 minutes of play, it is extended by 30 additional minutes. If it is still tied after this extra time, a penalty shootout takes place. In the penalty shootout, the teams alternate in kicking a penalty kick. The sequence of kicks involves five kicks for each team, but it is extended if it ends with a tie. Each penalty kick is shot from a distance of 11 meters from the goal, against the opposite team’s goalkeeper, where no other players are allowed to stand in the way. The goalkeeper must remain on the goal-line until the kick is taken. The time it takes the ball to reach the goal from the penalty mark is only about 0.2–0.3 seconds (Chiappori, Levitt & Groseclose, Reference Chiappori, Levitt and Groseclose2002; Palacios-Huerta, Reference Palacios-Huerta2003). Consequently, the goalkeeper generally cannot wait to see to which direction the ball is kicked before choosing his action; rather, he must decide whether to jump to one of the sides or to stay in the goal’s center roughly at the same time that the kicker chooses how to kick (McMorris & Hauxwell, Reference McMorris, Hauxwell, Reilly, Bangsbo and Hughes1997; Savelsbergh et al., Reference Savelsbergh, Williams, Van der Kamp and Ward2002; Savelsbergh et al., Reference Savelsbergh, Van der Kamp, Williams and Ward2005). This is the source of the terminology that attributes to the goalkeeper “gambling” on which side the kicker will choose, and jumping to that side.
The goalkeepers try to seek clues (e.g., the position of the penalty-taker’s hips, kicking leg, and his trunk movements) regarding the direction towards which the ball will be shot (Tyldesley, Bootsma & Bomhoff, Reference Tyldesley, Bootsma, Bomhoff, Rieder, Bos, Mechling and Reische1982; Williams & Burwitz, Reference Williams, Burwitz, Reilly, Clarys and Stibbe1993). However, on the other side there is also a professional player, who can try to deceive and confuse the goalkeeper. At the end, the success of the goalkeeper to choose the correct side, that is, the same direction of the kick, is quite limited, and does not exceed by a lot what it would have been if the goalkeeper was choosing his action randomly (Palacios-Huerta, Reference Palacios-Huerta2003; Azar & Bar-Eli, Reference Azar and Bar-Eli2011).
The simultaneity of choice between the goalkeeper and the kicker, the speed of the ball, the unavailability of defending players and the large goal dimensions (2.44 meters high X 7.32 meters wide) make the goalkeeper’s task in penalty kicks remarkably difficult. As a result, most penalty kicks end with a goal. For example, in our sample of 500 penalty kicks, 71% end with a goal, and in Palacios-Huerta (Reference Palacios-Huerta2003) sample, 80% of the kicks end with a goal.
Game-theoretic models have viewed soccer penalty kicks as a zero-sum, simultaneous-move game. Analyses of penalty kicks (mostly during the game) have suggested that goalkeepers and kickers both use a mixed strategy, choosing between left and right jumps or kicks randomly (or at least in a way that appears random to the other player, who cannot predict their choice) (Chiappori, Levitt & Groseclose, Reference Chiappori, Levitt and Groseclose2002; Palacios-Huerta, Reference Palacios-Huerta2003; Azar & Bar-Eli, Reference Azar and Bar-Eli2011). Standing still (i.e., choosing “center”) is a strategy rarely used by the goalkeepers (Bar-Eli et al., Reference Bar-Eli, Azar, Ritov, Keidar-Levin and Schein2007). The mixed-strategy Nash equilibrium that penalty kicks yield in the samples used in the above studies can hold only if both goalkeepers’ and kickers’ choices are serially independent and uncorrelated, because any predictable pattern of sequential behavior (i.e., any departure from randomness) could be exploited by the other player. Indeed, penalty kicks were found to be random and serially independent and do not show regular patterns of kicking direction (Chiappori, Levitt & Groseclose, Reference Chiappori, Levitt and Groseclose2002; Palacios-Huerta, Reference Palacios-Huerta2003).
1.3 The gambler’s fallacy in penalty kick shootouts
Professional sports provide an interesting arena to examine various issues in decision making, thanks to a few important advantages. The rules of the game are generally clear, the relevant players are well-defined, the players are experienced and have huge financial motivations to make their best decisions, and abundant data exist (though sometimes a large effort is required to collect them and convert them to a form that can be analyzed). One of the sports that attracted much attention, being a highly popular sport in many countries, is soccer. In soccer, the penalty kick situation has been studied due to its clear and constant characteristics and relative simplicity (the same location of the ball in all penalties, no need to consider the exact location of 22 players, etc.).
Within the discussion on goalkeepers’ suboptimal behavior during penalty kicks (e.g., Bar-Eli et al., Reference Bar-Eli, Azar, Ritov, Keidar-Levin and Schein2007; Roskes et al., Reference Roskes, Sligte, Shalvi and De Dreu2011; Memmert et al., Reference Memmert, Hüttermann, Hagemann, Loffing and Strauss2013), a recent study by Misirlisoy and Haggard (Reference Misirlisoy and Haggard2014) reported that goalkeepers display a clear sequential bias. Following repeated kicks in the same direction, goalkeepers subject to the gambler’s fallacy became increasingly likely to dive in the opposite direction on the next kick. Kickers showed less predictable behavioral sequences, revealing smaller gambler’s fallacy patterns.
Here we argue first, that in such analyses, the goal center width must be taken into account, and should be objectively defined in advance. We show that the definition of the goal center width might have a major effect on the distribution of kicks and kicking sequences (i.e., how many sequences of a certain length are recorded in the data), and thus on the results obtained. Second, we suggest that a different treatment of sequences is required to account for potentially limited cognitive abilities (and in particular memory) of the goalkeeper. We demonstrate our arguments through the case of the gambler’s fallacy reported by Misirlisoy and Haggard (Reference Misirlisoy and Haggard2014), using different goal center widths and a different treatment of sequences as will be described below.
Misirlisoy and Haggard (Reference Misirlisoy and Haggard2014) removed from their analyses the penalties for which either the goalkeeper or the kicker chose the center. They did not explain, however, how the center was defined. It is reasonable to assume that, while coding the kicks’ direction, they adopted an imaginary zone down the middle of the goal, represented by the goalkeeper’s immediate reach to the left or right when standing at the centerline. They coded a ’center dive’ when the goalkeeper remained in his starting position and did not dive to either side. The as yet undefined width of this imaginary zone may affect the kick distribution and the respective conclusions. They identified 16 cases that involved sequences of three kicks to the same direction. In 11 of these cases, in the kick that followed, the goalkeepers dived to the opposite direction, possibly reflecting a belief that the sequence of three kicks to the same direction will end with a kick to the opposite side. Based on bootstrap analysis of these 16 cases, Misirlisoy and Haggard concluded that goalkeepers exhibited the gambler’s fallacy.
1.4 Limitations
Braun and Schmidt (Reference Braun and Schmidt2015) argued that penalty shootouts may not be an appropriate setting for analyzing the gambler’s fallacy because the environment is not random. Ideally, an analysis in the context of shootouts would require data where both goalkeepers’ and kickers’ choices are completely independent. However, as Braun and Schmidt described, good kickers are often able to shoot in the direction opposite to the dive direction of the goalkeeper. In addition, the order of kickers in shootouts may not be random. This fact could be particularly problematic, as behavior after a series of successive shots in the same direction can be observed only towards the end of the shootout when often the best penalty shooters line up (Jordet et al., Reference Jordet, Hartman, Visscher and Lemmink2007). Recent studies have pointed to additional factors that might affect penalty shootout scores, such as kicking order (first versus second kicking team in the shootout; Apesteguia & Palacios-Huerta, Reference Apesteguia and Palacios-Huerta2010), and the difference between the two teams’ scores immediately before each kick (Price & Wolfers, Reference Price and Wolfers2014; Roskes et al., Reference Roskes, Sligte, Shalvi and De Dreu2011).
A potential additional bias is that kickers tend to use the inside of their dominant foot to make contact with the ball during a penalty kick. This means that right-footed kickers have different probabilities to shoot left or right compared to left-footed kickers (Chiappori, Levitt & Groseclose, Reference Chiappori, Levitt and Groseclose2002; Palacios-Huerta, Reference Palacios-Huerta2003). A goalkeeper may use information about the kicker’s “natural side” in deciding which way to dive.
To address these potential flaws, Braun and Schmidt (Reference Braun and Schmidt2015) ran a computerized laboratory experiment in which decisions of kickers and goalkeepers were fully independent. Penalties were performed sequentially as in a real shootout, but in a completely random environment. For each penalty, the goalkeeper and the kicker chose simultaneously and independently one side (left or right). The results showed that in this ideal setting, the gambler’s fallacy could not be observed.
Indeed, laboratory settings have advantages regarding randomness over real-world contexts, where full randomness is hard to achieve. However, there are also important advantages to real-world contexts. Decisions are in a real environment and not in an artificial one, incentives are substantial and not negligible as in many lab experiments, and decision makers are top professionals and not young students. Therefore, we believe that our approach of taking penalties from the world’s top soccer competitions and analyzing them is a worthwhile endeavor despite the fact that this environment is not completely random. The two approaches, of lab experiments and data from the real world, are complementary, each with its advantages and disadvantages.
There are many other studies on sports (e.g., Apesteguia & Palacios-Huerta, Reference Apesteguia and Palacios-Huerta2010; Kocher, Lenz & Sutter, Reference Kocher, Lenz and Sutter2012; Massey & Thaler, Reference Massey and Thaler2013; Walker & Wooders, Reference Walker and Wooders2001) that further show that the advantages of the real-world context are important, even though their data also include many uncontrolled factors that affect players as in our data. We argue that even if there are factors that may affect the kicker’s choice of side in penalty kicks, he would have to hide any tendency to kick to one of the sides, so that his choice remains as unpredictable as possible in order not to give the goalkeeper an advantage. Thus, the actual kick direction, at least from the perspective of the goalkeeper, is random. We believe that arguing that the goalkeeper cannot predict the direction of the kick is a fairly good approximation, and therefore the gambler’s fallacy is relevant.
For our analysis of shootouts, we did not attempt to control for everything that is not random in this setting. We were interested to examine whether, after a stimulus of a certain sequence of previous kicks, goalkeepers are more likely to jump to the same side or the opposite one. It was not our purpose to use everything possible to try to predict to which side they will jump, but rather only to examine the impact of the particular stimulus we analyze (which is related to the gambler’s fallacy).
Finally, it could be argued that familiarity of the goalkeeper with the kicking player might cause deviation from randomness. While this is possible for a small group of individuals, it is rather almost impossible for the goalkeeper to remember the record of hundreds of players who played in different tournaments, in different periods and against different teams. Since penalty shootouts in soccer are relatively rare, the interaction between the goalkeeper and each individual kicking player is even more seldom. Moreover, as noted above, kickers try to show less predictable behavioral choices, in order not to let the goalkeeper anticipate the direction of the kick. Therefore, we argue that the effect of familiarity is not enough to undermine the use of shootouts as a valid setting to examine whether goalkeepers follow the gambler’s fallacy.
2 Method
To demonstrate our arguments, we collected data independently on the same sample of 361 kicks used in Misirlisoy and Haggard (Reference Misirlisoy and Haggard2014). This dataset includes all kicks that occurred in FIFA World Cup and UEFA Euro Cup finals over the period from 1976 to 2012. We employed an objective approach for mapping the kicks’ exact directions. Online videos provide spectators with different angles of photo for each kicked ball, mainly front view, back view, and occasionally also some other side view. We based our coding in most cases on the back view of the goal. Our coding procedure involved precise measurements of the coordinates for each kick while the ball was crossing the goal plane (i.e., the distance of the ball from the right side and the upper bar of the goal were measured, as viewed on the screen). Penalties are kicked from 11 meters towards a 7.32 by 2.44 meter goal, and the depth of the goal is 3.05 meters (i.e., the distance of the net from the goal line). We found that in most cases the trajectory of the ball into the goal is a straight line, rather than a curve route (balls shot towards the goal may reach speeds of over 80 km/h). Using a simple algorithm, we then transformed the raw data collected from the videos into the actual dimensions of the goal. This approach gave us for each kick the exact distance from the ball to the ground and to the goal posts when the ball was reaching the goal plane. For off-target shots kicked outside the net, we manually calculated the location of the ball around the goal’s frame. We also coded the goalkeeper’s dive direction (left/right/center) for each kick.
Our mapping method allowed us to flexibly determine the goal center width, and thus to extract the corresponding numbers of kicks shot to the left, right and center. For example, while Misirlisoy and Haggard (Reference Misirlisoy and Haggard2014) reported that kicks to the center were very rare (9.14%), an earlier study, where the center was defined as the central third, found that 28.7% kicks were directed to the center (Bar-Eli & Azar, Reference Bar-Eli and Azar2009). Using our method for mapping kicks’ directions, we found that a goal center width of 66 cm (i.e., 33 cm on each side of the exact center) corresponds to the low number reported by Misirlisoy and Haggard (9.14%). When we examined instead a center width of 240 cm (i.e., about a third of the goal), which is roughly the area in the goalkeeper’s immediate reach (opening his hands, making small body movements without diving or walking to the side; Ziv & Lidor, Reference Ziv and Lidor2011), we found 82 kicks (22.7%) directed to the center.
3 Results and discussion
We extended the analysis reported in the previous literature (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014; Braun & Schmidt, Reference Braun and Schmidt2015) in several ways. First, we collected our data independently, using videos of the relevant penalty kick shootouts, without relying on previous datasets. Second, we not only categorize if a kick is to the left, right or center, but also know the exact distance of the ball (in the resolution of centimeters) from the goal’s center, allowing us to analyze the results for various measures of the goal center width. Third, after analyzing the sample of the same 361 penalty kicks that were analyzed previously (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014), we extended the sample to 500 penalty kicks (more details about this extension will be mentioned below).
Fourth, we change the way center kicks affect the sequence. A sequence means a number of consecutive kicks that are all to the same side. Let us use a coding in which the left-most letter is the first kick in the sequence considered, the next letter is the kick after it, and so on, and R stands for right, C for center, L for left." We consider a kick to the center as breaking a sequence and do not ignore it as Misirlisoy & Haggard (Reference Misirlisoy and Haggard2014) do, which means that in our data, RCR is not the same as RR. That is, after a kick to the right, then the center, then again to the right, we do not think that the goalkeeper remembers a sequence of two consecutive kicks to the right and forgets that in between there was a kick to the center, as implied by the treatment of center in Misirlisoy & Haggard (Reference Misirlisoy and Haggard2014). Instead, since the goalkeeper remembers the center kick before the last right kick, he views the sequence as one kick to the right, with a different direction before that. We believe that this is a more appropriate treatment that matches better the information structure that the goalkeeper responds to.
Finally, we used two alternative methods to count sequences. One sequence-counting method we used is to eliminate from sequences of length X those that are part of a longer sequence (e.g., RLL will be considered as a sequence of two kicks to the left, but LLL will not be a 2-kicks sequence because it is part of a sequence of three kicks). This is in line with previous studies, and it implies that sequences of length X are determined considering X+1 kicks. The second method is to look only at the last X kicks when deciding whether it is a sequence of length X (e.g., both RLL and LLL will be considered as having LL sequence).
The directions of right and left are always from the goalkeeper’s perspective, both for the kicks and for the goalkeeper jumps. This means that a jump to the left and a kick to the left are to the same side of the goal, not to opposite sides. To test for the gambler’s fallacy, we examined the effects of repeated ball direction across consecutive kicks on goalkeepers’ behavior, for different goal center widths. A gambler’s fallacy in this context means, for example, that the goalkeeper will believe that after a sequence of kicks to the left, the next kick is more likely to be to the right. Therefore he should jump to the right.
The tables that summarize our analysis are built as follows. We count the number of jumps to each side. The jumps that are to the same side of the recent sequence (the sequence does not include the current kick, to reflect the same information that the goalkeeper has at the time of making his decision) are called “Jumps to same direction”. The jumps to the opposite side of the recent sequence are called “Jumps to opposite direction”. We then consider the “% of jumps to opposite direction”. Without a gambler’s fallacy, this percentage should be around 50%. With a gambler’s fallacy, it should be higher than 50%, reflecting the goalkeeper’s belief that the kick is more likely to be to the opposite side of a recent sequence than to be to the same side and extend the sequence even further. We test whether the “% of jumps to opposite direction” is different from 50% using a binomial test, and report the 1-tailed p-value of this test.Footnote 1
3.1 Analysis of the 361 kicks, sequences are determined considering X+1 kicks
We first report the results obtained with the same approach for counting sequences as in the previous literature, i.e., eliminating from the count of sequences of length X those that are part of a sequence of length X+1 (e.g., LLL will not be considered also as sequence of two kicks to the left), for the sample of 361 kicks. The results are presented in Table 1. The table (and the following ones) consider jumps to the same direction as the recent sequence versus jumps to the opposite direction, omitting cases in which the goalkeeper stayed in the center. This allows to have a clear testable prediction, namely that in the absence of gambler’s fallacy of the goalkeepers, we should see the two actions (same or opposite direction) being chosen with about 50%:50% chances.Footnote 2
Table 1: Goalkeeper dive direction for different goal center widths, sequences are determined considering X+1 kicks (n=361 kicks)
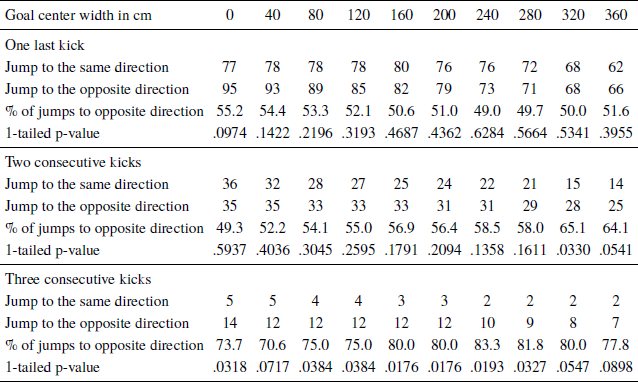
For a sequence of one kick, the gambler’s fallacy could not be detected for any goal center width. However, for two consecutive kicks directed to the same side, the gambler’s fallacy could be detected for a goal center width of 320 cm (p = .0330), but not for the other center widths. This result is not in line with previous studies (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014; Braun & Schmidt, Reference Braun and Schmidt2015), which reported that the gambler’s fallacy could not be detected in the case of two consecutive kicks.
Regarding three consecutive kicks shot to the same side, our results show that for any goal center width between 80–280 cm, the goalkeeper dived in the opposite direction of the last three kicks in at least 75% of the cases (p < .05). These results are in line with Misirlisoy & Haggard (Reference Misirlisoy and Haggard2014), who also find evidence for the gambler’s fallacy after sequences of three kicks (using bootstrapping methods and not the binomial test). However, interestingly our results are not in line with the re-analysis of Misirlisoy & Haggard (Reference Misirlisoy and Haggard2014) data by Braun & Schmidt (Reference Braun and Schmidt2015), who used the binomial test as we do. The different results can be the outcome of the different data collection we followed: we collected the data independently, did not erase center kicks or jumps (which means that RCR kicks is not an RR sequence in our data, but it is in Misirlisoy & Haggard (Reference Misirlisoy and Haggard2014)), and we analyze the different goal center widths, which was not done before. We also find that for a zero center zone width (where only right and left sides exist), the results are also in line with the gambler’s fallacy (p=.0318). For goal center width of 40 cm or 320–360 cm, the gambler’s fallacy cannot be detected at the 5% level. Overall, the results that different center widths in the sequences of two and three kicks can lead to different conclusions illustrate the importance of an a priori definition of the goal center width before analyzing the data.
3.2 Analysis of the 361 kicks, sequences are determined considering X kicks
The previous section defines sequences in manner similar to previous studies (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014; Braun & Schmidt, Reference Braun and Schmidt2015). A sequence of length X is considered as such only if it is not part of a sequence of length X+1. When we see RR (the two last kicks are to the right), we still do not know if this is a sequence of length two or not. Assuming that there were three or more kicks already, to decide whether we have a sequence of two we also need to check the kick before the last two. If we find that the RR was part of LRR (the kick before the last two ones was to the left), then it is a sequence of two. However, if the RR was part of RRR, it is not considered as a sequence of two because it is part of a sequence of three. We denote this approach for counting sequences “considering X+1 kicks”. While we can come up with some justification for this approach, we believe that another reasonable approach is to define a sequence of length X only using the last X kicks without going also to the preceding kick. For example, if the goalkeeper, under the tremendous pressure of a penalty shootout in a top match, has difficulty remembering or analyzing the kick that happened before the three last ones, then it means that he considers a sequence of three kicks to the right both if it was RRRR or LRRR. Then, we need to consider only the X last kicks to determine whether there is a sequence of X kicks, and we no longer need to go to kicks before the last X; in the above example, RRR tells us that we have a sequence of three kicks to the right. We denote this alternative approach for counting sequences “considering X kicks”.
To address this alternative manner of defining sequences, we analyzed the data once again, using this time a definition of sequences as explained above. That is, a sequence of length X exists whenever the last X kicks were to the same direction, regardless of what happened in the kick before the last X kicks. Table 2 below presents the results, for the same sample of 361 kicks.
Table 2: Goalkeeper dive direction for different goal center widths, sequences are determined considering X kicks (n=361 kicks)
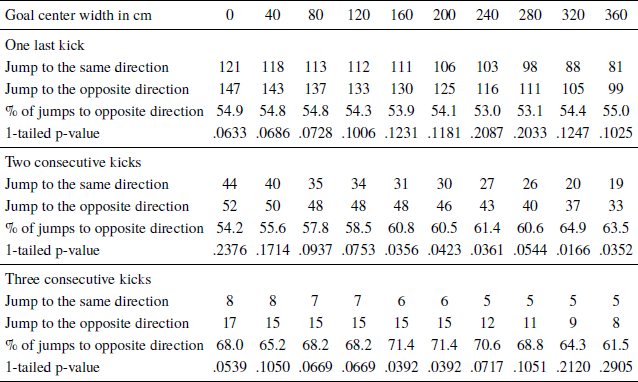
For sequences of one kick, the gambler’s fallacy could not be detected for any goal center width. However, for sequences of two kicks, the gambler’s fallacy could significantly be detected for any goal center width of 160 cm (p = .0356) or above, but not for smaller goal center widths. This finding does not support the results reported in previous studies (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014; Braun & Schmidt, Reference Braun and Schmidt2015), according to which the gambler’s fallacy could not significantly be detected in the case of two consecutive kicks.
Regarding three consecutive kicks shot to the same side, our results confirm the gambler’s fallacy effect only for goal center widths of 160 cm or 200 cm. Within this interval, in 15 out of 21 cases (71%), the goalkeepers jump to the opposite direction of the sequence, which is significantly higher than a random choice of 50% (p = .0392).
The results in Table 2 demonstrate once again that the existence of a sequential bias in the diving behavior of goalkeepers depends on how the goal center width is defined. The results also suggest that if we adopt a different way to define a sequence (i.e., define a sequence of length X only using the last X kicks without considering also the preceding kick), then a significant gambler’s fallacy could be detected not only after sequences of three consecutive kicks, but also after sequences of two kicks to the same side, a result that previous studies (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014; Braun & Schmidt, Reference Braun and Schmidt2015) failed to show. For example, when a center width of 240 cm is selected (i.e., a central third that is represented by the goalkeeper’s immediate reach when standing at the goal center), then in 43 out of 70 cases (61%) the dive was in the opposite direction to the last two kicks, a higher percentage than the random chance of 50%, where the difference is statistically significant (p = .0361).
3.3 Analysis of 500 kicks, sequences are determined considering X+1 kicks
To further examine the robustness of our results, we extended our dataset of 361 kicks to include the 2014 FIFA World Cup (36 kicks) and the Champions League from 1984 to 2012 (103 kicks), resulting in a total of 500 kicks. We first report the results obtained with the same approach for counting sequences as in the previous literature, i.e., eliminating from the count of sequences of length X those that are part of a longer sequence (e.g., RLL will be considered as sequence of two kicks to the left, but not LLL). The results are presented in Table 3.
Table 3: Goalkeeper dive direction for different goal center widths, sequences are determine considering X+1 kicks (n=500 kicks)
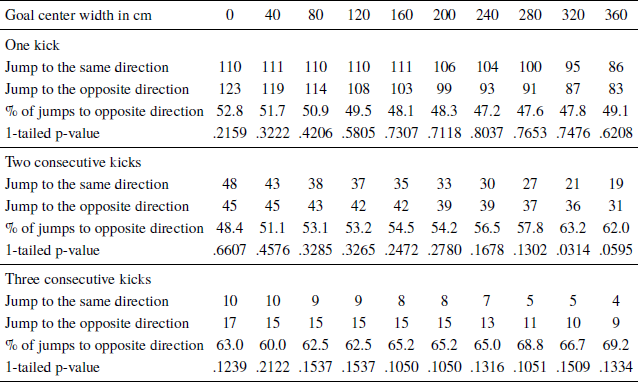
For sequences of one kick, the gambler’s fallacy could not be detected for any goal center width. For two consecutive kicks directed to the same side, the gambler’s fallacy could be detected only for goal center width of 320 cm (p = .0314), but not for the other center widths. For sequences of three consecutive kicks shot to the same side, our results do not show a gambler’s fallacy significant at the 5% (or even 10%) level, for any goal center width.
Our results do, however, indicate that after a sequence of three consecutive kicks, goalkeepers are more likely to dive to the other side (at probabilities ranging between 60% and 69.2% for different center widths). Thus, the data for three kicks seemingly show a tendency in the direction predicted by the gambler’s fallacy, but with a limited number of observations, which makes it difficult to reach statistical significance. Consequently, despite the large probability gap (60%–69.2% vs. the complementary probability of 30.8%-40%), this difference is not statistically significant. Therefore, based on the current data, we cannot conclude that a gambler’s fallacy exists, and further investigations using a greater number of observations (especially for three consecutive kicks) are required to support the gambler’s fallacy in goalkeepers’ behavior.
3.4 Analysis of 500 kicks, sequences are determined considering X kicks
We now turn to the alternative treatment of sequences (looking only at the X last kicks when deciding whether it is a sequence of length X), which was described earlier, for the same sample of 500 kicks. Table 4 shows the results.
Table 4: Goalkeeper dive direction for different goal center widths, sequences are determined considering X kicks (n=500 kicks)
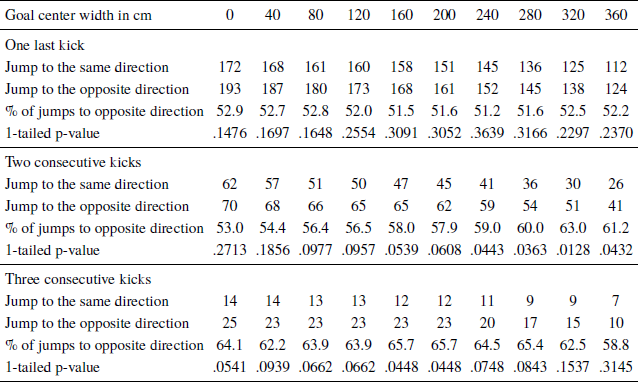
For sequences of one kick, the gambler’s fallacy could not be detected for any goal center width. However, for sequences of two consecutive kicks directed to the same side, the gambler’s fallacy could significantly be detected for goal center width of 240 cm (p = .0443) or larger. For goal center widths between 80 cm and 200 cm, the gambler’s fallacy is not quite significant.
Regarding sequences of three consecutive kicks shot to the same side, our results confirm the existence of a gambler’s fallacy at the 5% level, only for center widths between 160 cm and 200 cm. In these cases, in 23 out of 35 cases (66%), the goalkeeper dived in the opposite direction of the last three consecutive kicks, resulting in a statistically significant gambler’s fallacy (p = .0448). It is important to note, however, that for any center width up to 280 cm, the results are consistent with the gambler’s fallacy but at a significance level of 10% and not 5% (except for 160–200 cm where the 5% level holds). Interestingly, for sequences of two kicks the only center widths for which the gambler’s fallacy cannot be detected even at the 10% level are the shortest ones (0–40 cm), whereas for sequences of three kicks this is true for the longest widths (320–360 cm). The evidence in Table 4 for a significant gambler’s fallacy even after a sequence of only two kicks, stands in some contrast to the literature, which suggests that a run of at least three repeated events is needed for people to perceive streaks and for the gambler’s fallacy to occur (Carlson & Shu, Reference Carlson and Shu2007).
The results in Table 4 suggest again that the goal center width has an important role in detecting the gambler’s fallacy in the diving behavior of goalkeepers. The results also show the relevance of how sequences are being counted. Some earlier studies did not even specify how they count sequences and it required looking directly at their data to realize that they used the method of looking at X+1 kicks to determine sequences of length X. We show here that this choice is not innocuous and it can seriously affect the results and conclusions even with the exact same data, as the differences between Table 3 and Table 4 (and also between Table 1 and Table 2) reveal. For example, if we limit attention to center widths of 0–280 cm and sequences of two or three kicks, Table 3 suggests that the gambler’s fallacy cannot be detected for any width even at the 10% level, whereas Table 4 shows almost the exact opposite, with a gambler’s fallacy at the 10% level almost everywhere.
4 Conclusions
Using either the same 361 penalty kicks as in Misirlisoy and Haggard’s (Reference Misirlisoy and Haggard2014) study (but independently collected and analyzed) or our extended data of 500 kicks, we find that the existence of a statistically significant sequential bias in goalkeepers’ diving behavior depends on how the goal center width is defined. We therefore demonstrate the advantage of our approach, which measures objectively and accurately the location of the ball when crossing the goal plane, over subjective approaches used earlier, which let judges only choose whether the kick was to the right, center or left, often without a clear definition of what the center is. Our approach not only allows replication more than vague and subjective measures of the center, but also it allows analyzing the data for different definitions of center, as we do. This analysis can show how sensitive the results are to the definition of the center width.
We further propose a different manner to count sequences, based only on the relevant number of kicks without considering the kick that preceded the sequence length, and show that this change is also important and can affect the results and the conclusions. This alternative method to count sequences makes sense for various reasons, for example if the goalkeeper reacts to a sequence of a certain length and cannot remember longer sequences (which is reasonable given the pressure on the goalkeeper, the cognitive load of trying to obtain cues from the kicker’s behavior and of trying to remember the history of the kicker’s penalties in previous games, etc.). The same idea can be applied for counting sequences in other cases, for example the kickers in penalty kicks, gamblers in the roulette, or other decision makers in various contexts.
We offer many different analyses and show how the results and conclusions may change, but it is useful also to discuss here briefly the overall tendencies reflected in the data. Finding a gambler’s fallacy that is statistically significant depends crucially on the sample, the sequence-counting method, the length of the sequence and the center width. But if we only look at the direction of behavior without its statistical significance, the pattern of behavior is much more consistent across the various analyses, and it supports the idea that goalkeepers display a gambler’s fallacy in penalty kick shootouts. In particular, the extended sample of kicks (Tables 3 and 4) yields statistically significant evidence for gambler’s fallacy of the goalkeepers for various center widths. Moreover, for the vast majority of sequence lengths and center widths, for the two samples, and regardless of which of the two sequence-counting methods we use, we find that the percentage of jumps to the opposite direction is higher than 50%. In particular, out of 120 computations of the percentage of jumps to the opposite direction in Tables 1–4, in 109 cases it is above 50% (the largest value being 83.3%), but only in 11 cases it is below 50%, and even then not far from 50% (the lowest value is 47.2%). For the sequence-counting method that we propose where the kick before the last X kicks is not considered when finding sequences of length X, in all 60 computations the percentage is higher than 50%. Alternatively, considering both sequence-counting methods but eliminating the sequences of one kick (which is extremely short and therefore unlikely to yield a gambler’s fallacy), in only 2 of the 80 computations the percentage is lower than 50% (and both of these cases are for the extreme center width of 0 cm). These patterns of behavior reflect a clear tendency of goalkeepers to dive to the opposite direction of the recent sequence of kicks, in line with the gambler’s fallacy. This conclusion is consistent with previous research (Misirlisoy & Haggard, Reference Misirlisoy and Haggard2014). However, Misirlisoy & Haggard find evidence for the gambler’s fallacy only in sequences of three kicks, whereas we show that it exists in various cases also for sequences of two kicks. Based on these patterns, it can be concluded that kickers should be advised to shoot in the same direction as the previous kicker of their team did, as suggested by Braun & Schmidt (Reference Braun and Schmidt2015).
As with any real-world data, a limitation of our data is that in addition to the variables we analyze, there are additional factors that change at the same time, which cannot be controlled. Lab experiments are a way to solve such problems and indeed are an important complementary methodology to empirical studies or natural experiments. Still, there are important advantages to real-world data that imply that studies using such data are also essential. In particular, their external validity is higher than that of artificial lab experiments, they often provide high-powered incentives that are hard to achieve in lab experiments, and often involve experienced or even professional decision makers.
Our results provide evidence for the gambler’s fallacy at the highest levels of international soccer, with goalkeepers who are the best in their countries and among the best in the world and have huge incentives to perform the best they can. This finding adds to a list of studies that show not only that deviations from full rationality in behavior exist, but also that they can persist with experienced decision makers or large incentives. Sports provide ideal arena to examine certain behaviors due to the experienced and highly-motivated players, clear rules of the game, and abundant public data (e.g., Cohen-Zada et al., Reference Cohen-Zada, Krumer and Shtudiner2017; Cohen-Zada, Krumer & Shtudiner, Reference Cohen-Zada, Krumer and Shtudiner2017). We hope that this study will encourage others to study the gambler’s fallacy and additional biases in professional sports.






