Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:07:25.536Z Has data issue: false hasContentIssue false
  • English
  • Français

SMOOTH BIMODULES AND COHOMOLOGY OF II1 FACTORS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  07 May 2015

Alin Galatan  and
Sorin Popa
Alin Galatan
Affiliation:
Department of Mathematics, University of California, UCLA, Los Angeles, CA 90095-1555, USA ([email protected]; [email protected])
Sorin Popa
Affiliation:
Department of Mathematics, University of California, UCLA, Los Angeles, CA 90095-1555, USA ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, under rather general conditions, the 1-cohomology of a von Neumann algebra 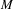$M$ with values in a Banach 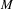$M$ -bimodule satisfying a combination of smoothness and operatorial conditions vanishes. For instance, we show that, if 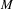$M$ acts normally on a Hilbert space 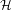${\mathcal{H}}$ and 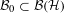${\mathcal{B}}_{0}\subset {\mathcal{B}}({\mathcal{H}})$ is a norm closed 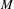$M$ -bimodule such that any 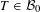$T\in {\mathcal{B}}_{0}$ is smooth (i.e., the left and right multiplications of $T$ by 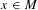$x\in M$ are continuous from the unit ball of 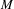$M$ with the 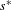$s^{\ast }$ -topology to 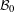${\mathcal{B}}_{0}$ with its norm), then any derivation of 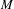$M$ into 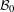${\mathcal{B}}_{0}$ is inner. The compact operators are smooth over any 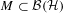$M\subset {\mathcal{B}}({\mathcal{H}})$ , but there is a large variety of non-compact smooth elements as well.

Keywords

von Neumann II1factorscohomologyderivationssmooth bimodules

MSC classification

Primary: 46L10: General theory of von Neumann algebras 46L57: Derivations, dissipations and positive semigroups in $C^*$-algebras
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 1 , February 2017 , pp. 155 - 187
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akemann, C. E. and Ostrand, P. A., Computing norms in group C ∗ -algebras, Amer. J. Math. 98 (1976), 1015–1047.CrossRefGoogle Scholar
Alekseev, V., On the first continuous $L^{2}$ -cohomology of free group factors. arXiv:1312.5647.Google Scholar
Alekseev, V. and Kyed, D., Measure continuous derivations on von Neumann algebras and applications to $L^{2}$ -cohomology. arXiv:1110.6155.Google Scholar
Bader, U., Gelander, T. and Monod, N., A fixed point theorem for L 1 spaces, Invent. Math. 189 (2012), 143–148.CrossRefGoogle Scholar
Bozejko, M., On 𝛬(p) sets with minimal constant in discrete noncommutative groups, Proc. Amer. Math. Soc. 51 (1975), 407–412.Google Scholar
Christensen, E., Derivations and Their Extensions to Perturbations of Operator Algebras, Proceedings of Symposia in Pure Mathematics, Volume 38, pp. 261–273 (American Mathematical Society, Providence, RI, 1982).Google Scholar
Connes, A., On the Classification of von Neumann Algebras and Their Automorphisms, Symposia Mathematica, Volume XX, pp. 435–478 (Academic Press, London, 1976).Google Scholar
Connes, A. and Shlyakhtenko, D., L 2 -homology for von Neumann algebras, J. Reine Angew. Math. 586 (2005), 125–168.Google Scholar
Dixmier, J., Les algebres d’operateurs dans l’espace hilbertien (Gauthier-Villars, Paris, 1957), 1996.Google Scholar
Dykema, K., Two applications of free entropy, Math. Ann. 308 (1997), 545–558.Google Scholar
Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology, and von Neumann algebras I, II, Trans. Amer. Math. Soc. 234 (1977), 289–324. 325–359.Google Scholar
Gaboriau, D., Invariants ℓ 2 de rélations d’équivalence et de groupes, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 93–150.Google Scholar
Haagerup, U., All nuclear C ∗ -algebras are amenable, Invent. Math. 74 (1983), 305–319.Google Scholar
Ioana, A., Peterson, J. and Popa, S., Amalgamated free products of w-rigid factors and calculation of their symmetry groups, Acta Math. 200 (2008), 85–153. arXiv:math.OA/0505589.Google Scholar
Johnson, B. E., Kadison, R. V. and Ringrose, J. R. , Cohomology of operator algebras III: reduction to normal cohomology, Bull. Soc. Math. France 100 (1972), 73–96.Google Scholar
Johnson, B. and Parrott, S., Operators commuting with a von Neumann algebra modulo the set of compact operators, J. Funct. Anal. 11 (1972), 39–61.Google Scholar
Kadison, R. V. and Ringrose, J. R. , Cohomology of operator algebras I: type I von Neumann algebras, Acta Math. 126 (1971), 227–243.Google Scholar
Kadison, R. V. and Ringrose, J. R., Cohomology of operator algebras II: extended cobounding and the hyperfinite case, Ark. Mat. 9 (1971), 55–63.Google Scholar
Kesten, H., Symmetric random walks on groups, Trans. Amer. Math. Soc. 92 (1959), 336–354.Google Scholar
Kirchberg, E., The derivation problem and the similarity problem are equivalent, J. Operator Theory 36 (1996), 59–62.Google Scholar
Murray, F. and von Neumann, J., Rings of operators IV, Ann. of Math. (2) 44 (1943), 716–808.Google Scholar
Peterson, J., L 2 -rigidity in von Neumann algebras, Invent. Math. 175 (2009), 417–433.Google Scholar
Peterson, J. and Thom, A., Group cocycles and the ring of affiliated operators, Invent. Math. 185 (2011), 561–592.Google Scholar
Pisier, G., Factorizations of Linear Operators and the Geometry of Banach Spaces, CBMS Lecture Notes, Volume 60 (1986).Google Scholar
Pisier, G., Introduction to Operator Space Theory, London Mathematical Society Lecture Notes, Volume 294 (2013).Google Scholar
Pisier, G., Similarity Problems and Completely Bounded Maps, Springer Lecture Notes, Volume 1618 (1995).Google Scholar
Pisier, G., Private communication.Google Scholar
Popa, S., On a problem of RV Kadison on maximal abelian *-subalgebras in factors, Invent. Math. 65 (1981), 269–281.Google Scholar
Popa, S., On derivations into the compacts and some properties of type II factors, in Proceedings of XIV-th Conference in Operator Theory, Herculane–Timisoara 1983 (ed. I. Gohberg), Volume 14, pp. 221–227 (Birkhäuser Verlag, 1984).Google Scholar
Popa, S., The commutant modulo the set of compact operators of a von Neumann algebra, J. Funct. Anal. 71 (1987), 393–408.Google Scholar
Popa, S., Free independent sequences in type II1 factors and related problems, Astérisque 232 (1995), 187–202.Google Scholar
Popa, S., Some computations of 1-cohomology groups and construction of non orbit equivalent actions, J. Inst. Math. Jussieu 5 (2006), 309–332. arXiv:mathOA/0407199.Google Scholar
Popa, S., A II1 factor approach to the Kadison–Singer problem, Comm. Math. Phys. (2014). arXiv:1303.1424.Google Scholar
Popa, S., Independence properties in subalgebras of ultraproduct II1 factors, J. Funct. Anal. 266 (2014), 5818–5846. arXiv:mathOA/1308.3982.Google Scholar
Popa, S., Classification of amenable subfactors of type II, Acta Math. 172 (1994), 163–255.Google Scholar
Popa, S. and Radulescu, F., Derivations of von Neumann factors into the compact ideal space of a semifinite algebra, Duke Math. J. 57 (1988), 485–518.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Vanishing of the continuous first $L^{2}$ -cohomology for II1 factors, Int. Math. Res. Not. IMRN (2014). arXiv:mathOA/1401.1186.Google Scholar
Powers, R. and Størmer, E., Free states of the canonical anticommutation relations, Comm. Math. Phys. 16 (1970), 1–33.Google Scholar
Radulescu, F., Vanishing of H w 2(M, K(H)) for certain finite von Neumann algebras, Trans. Amer. Math. Soc. 326 (1991), 569–584.Google Scholar
Ringrose, J., Automatic continuity of derivations of operator algebras, J. Lond. Math. Soc. 5 (1972), 432–438.Google Scholar
Sinclair, A. M. and Smith, R. R., Hochschild Cohomology of von Neumann Algebras, London Mathematical Society Lecture Note Series, Volume 203 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Takesaki, M., Theory of Operator Algebras, I, Encyclopaedia of Mathematical Sciences, Volume 124 (Springer-Verlag, Berlin, 2002). Reprint of the first (1979) edition, Operator Algebras and Non-commutative Geometry, 5.Google Scholar
Thom, A., L 2 -cohomology for von Neumann algebras, GAFA 18 (2008), 51–70.Google Scholar