Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T07:23:29.373Z Has data issue: false hasContentIssue false
  • English
  • Français

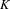VANISHING OF THE NEGATIVE HOMOTOPY $K$-THEORY OF QUOTIENT SINGULARITIES

Part of: $K$-theory in geometry Curves Local theory Higher algebraic $K$-theory Algebraic geometry: Foundations

Published online by Cambridge University Press:  08 May 2017

Gonçalo Tabuada
Gonçalo Tabuada*
Affiliation:
Department of Mathematics, MIT, Cambridge, MA 02139, USA Departamento de Matemática, FCT, UNL, Portugal Centro de Matemática e Aplicaçōes (CMA), FCT, UNL, Portugal ([email protected]) URL: http://math.mit.edu/∼tabuada
Get access Rights & Permissions [Opens in a new window]

Abstract

Making use of Gruson–Raynaud’s technique of ‘platification par éclatement’, Kerz and Strunk proved that the negative homotopy 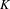$K$-theory groups of a Noetherian scheme 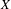$X$ of Krull dimension 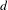$d$ vanish below 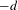$-d$. In this article, making use of noncommutative algebraic geometry, we improve this result in the case of quotient singularities by proving that the negative homotopy 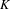$K$-theory groups vanish below 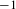$-1$. Furthermore, in the case of cyclic quotient singularities, we provide an explicit ‘upper bound’ for the first negative homotopy 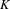$K$-theory group.

Keywords

K-theorysingularitiesnoncommutative algebraic geometry

MSC classification

Primary: 14A22: Noncommutative algebraic geometry 14B05: Singularities 14H20: Singularities, local rings 19E08: $K$-theory of schemes 19D35: Negative $K$-theory, NK and Nil
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 3 , May 2019 , pp. 619 - 627
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by the National Science Foundation Award #1350472 and by the Portuguese Foundation for Science and Technology grant PEst-OE/MAT/UI0297/2014.

References

Amiot, C., Iyama, O. and Reiten, I., Stable categories of Cohen–Macaulay modules and cluster categories, Amer. J. Math. 137(3) (2015), 813–857.Google Scholar
Böckstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compos. Math. 86 (1993), 209–234.Google Scholar
Buchweitz, R.-O., Maximal Cohen–Macaulay modules and Tate cohomology over Gorenstein rings. Available at https://tspace.library.utoronto.ca/handle/1807/16682.Google Scholar
Cortiñas, G., Haesemeyer, C., Schlichting, M. and Weibel, C., Cyclic homology, cdh-cohomology and negative K-theory, Ann. of Math. (2) 167(2) (2008), 549–573.Google Scholar
Gersten, S. M., Higher K-theory of rings, in Algebraic K-theory, I: Higher K-theories (Proc. Conf. Seattle Res. Center, Battelle Memorial Inst., 1972), Lecture Notes in Mathematics, Volume 341, pp. 3–42 (Springer, 1973).Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 361 pp.Google Scholar
Iyama, O. and Takahashi, R., Tilting and cluster tilting for quotient singularities, Math. Ann. 356(3) (2013), 1065–1105.Google Scholar
Keller, B., On triangulated orbit categories, Doc. Math. 10 (2005), 551–581.Google Scholar
Keller, B., On Differential Graded Categories, International Congress of Mathematicians, Volume II, pp. 151–190 (European Mathematical Society, Zürich, 2006).Google Scholar
Keller, B., Murfet, D. and Van den Bergh, M., On two examples by Iyama and Yoshino, Compos. Math. 147(2) (2011), 591–612.Google Scholar
Kerz, M. and Strunk, F., On the vanishing of negative homotopy K-theory, J. Pure Appl. Algebra 221(7) (2017), 1641–1644.Google Scholar
Kerz, M., Strunk, F. and Tamme, G., Algebraic $K$ -theory and descent for blow-ups, preprint, 2016. Available at arXiv:1611.08466.Google Scholar
Kurano, K. and Nishi, S., Gorenstein isolated quotient singularities of odd prime dimension are cyclic, Comm. Algebra 40(8) (2012), 3010–3020.Google Scholar
Lunts, V. and Orlov, D., Uniqueness of enhancement for triangulated categories, J. Amer. Math. Soc. 23 (2010), 853–908.Google Scholar
Orlov, D., Derived categories of coherent sheaves and triangulated categories of singularities, in Algebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin, II, Progress in Mathematics, Volume 270, pp. 503–531 (Birkhuser Boston, Inc., Boston, MA, 2009).Google Scholar
Reid, L., N-dimensional rings with an isolated singular point having nonzero K -N , J. K-theory 1 (1987), 197–205.Google Scholar
Rouquier, R., Dimensions of triangulated categories, J. K-Theory 1(2) (2008), 193–256.Google Scholar
Rouquier, R., Private e-mail exchange. August 2016.Google Scholar
Schlichting, M., Negative K-theory of derived categories, Math. Z. 253(1) (2006), 97–134.Google Scholar
Tabuada, G., Noncommutative Motives, University Lecture Series, Volume 63 (American Mathematical Society, Providence, RI, 2015). With a preface by Yuri I. Manin.Google Scholar
Tabuada, G., A1 -homotopy invariants of dg orbit categories, J. Algebra 434 (2015), 169–192.Google Scholar
Tabuada, G. and Van den Bergh, M., The Gysin triangle via localization and $\mathbb{A}^{1}$ -homotopy invariance, Trans. Amer. Math. Soc. (to appear), preprint, 2015. Available at arXiv:1510.04677.Google Scholar
Weibel, C., Mayer–Vietoris sequences and mod-p K-theory, Lecture Notes in Maths 966 (1983), 390–407.Google Scholar