Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T17:53:07.088Z Has data issue: false hasContentIssue false
  • English
  • Français

A geometric perspective on the Breuil–Mézard conjecture

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 June 2013

Matthew Emerton  and
Toby Gee
Matthew Emerton
Affiliation:
Mathematics Department, Northwestern University, 2033 Sheridan Rd., Evanston, IL 60208, USA ([email protected]; [email protected])
Toby Gee
Affiliation:
Mathematics Department, Northwestern University, 2033 Sheridan Rd., Evanston, IL 60208, USA ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

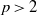Let $p\gt 2$ be prime. We state and prove (under mild hypotheses on the residual representation) a geometric refinement of the Breuil–Mézard conjecture for two-dimensional mod 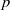$p$ representations of the absolute Galois group of 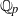${ \mathbb{Q} }_{p} $. We also state a conjectural generalization to $n$-dimensional representations of the absolute Galois group of an arbitrary finite extension of 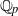${ \mathbb{Q} }_{p} $, and give a conditional proof of this conjecture, subject to a certain 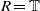$R= \mathbb{T} $-type theorem together with a strong version of the weight part of Serre’s conjecture for rank $n$ unitary groups. We deduce an unconditional result in the case of two-dimensional potentially Barsotti–Tate representations.

Keywords

automorphic formsGalois representations

MSC classification

Secondary: 11F33: Congruences for modular and $p$-adic modular forms
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 1 , January 2014 , pp. 183 - 223
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnet-Lamb, T., Gee, T. and Geraghty, D., The Sato–Tate conjecture for Hilbert modular forms, J. Amer. Math. Soc. 24 (2) (2011), 411–469.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Congruences between Hilbert modular forms: constructing ordinary lifts, Duke Math. J. 161 (8) (2012), 1521–1580.Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Serre weights for rank two unitary groups, Math. Ann. (2013), in press, doi:10.1007/s00208-012-0893-y.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Local-global compatibility for $l= p$, II, Ann. Sci. Èc. Norm. Supér. (2012), in press.Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) (2013), in press.CrossRefGoogle Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (1) (2011), 29–98.CrossRefGoogle Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups, Astérisque (324) (2009), xii+314.Google Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires et représentations de ${\mathrm{GL} }_{2} ({\mathbf{Z} }_{p} )$ et de $\mathrm{Gal} ({ \overline{\mathbf{Q} } }_{p} / {\mathbf{Q} }_{p} )$ en $l= p$, Duke Math. J. 115 (2) (2002), 205–310. With an appendix by Guy Henniart.Google Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires raffinées, Bull. Soc. Math. France (2012), in press.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod $l$ Galois representations over totally real fields, Duke Math. J. 155 (1) (2010), 105–161.CrossRefGoogle Scholar
Calegari, F., Even Galois representations and the Fontaine–Mazur conjecture. II, J. Amer. Math. Soc. 25 (2) (2012), 533–554.CrossRefGoogle Scholar
Caraiani, A., Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161 (12) (2012), 2311–2413.Google Scholar
Chenevier, G. and Harris, M., Construction of automorphic Galois representations, II, Cambridge Math. J. (2011), in press, http://intlpress.com/site/pub/pages/journals/items/cjm/content/vols/0001/0001/00026327/index.html.Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$ Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181.CrossRefGoogle Scholar
Conley, W., Inertial types and automorphic representations with prescribed ramification, PhD thesis, UCLA (2010).Google Scholar
Conley, W., In preparation, 2012.Google Scholar
Conrad, B., Diamond, F. and Taylor, R., Modularity of certain potentially Barsotti–Tate Galois representations, J. Amer. Math. Soc. 12 (2) (1999), 521–567.Google Scholar
Gee, T., A modularity lifting theorem for weight two Hilbert modular forms, Math. Res. Lett. 13 (5–6) (2006), 805–811.CrossRefGoogle Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350 (2011), 107–144, doi: 10.1007/s00208-010-0545-z.Google Scholar
Gee, T. and Kisin, M., The Breuil-Mézard conjecture for potentially Barsotti–Tate representations, preprint (2012).Google Scholar
Geraghty, D., Modularity lifting theorems for ordinary Galois representations, preprint (2009).Google Scholar
Guralnick, R., Adequate subgroups II, Bull. Math. Sci. 2 (1) (2012), 193–203.CrossRefGoogle Scholar
Guralnick, R. M., Adequacy of representations of finite groups of Lie type, Appendix A to Dieulefait’s paper ‘Automorphy of ${\mathrm{Symm} }^{5} (\mathrm{GL} (2))$ and base change’, (2012).Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, Volume 151 (Princeton University Press, Princeton, NJ, 2001). With an appendix by Vladimir G. Berkovich.Google Scholar
Herzig, F., The weight in a Serre-type conjecture for tame $n$-dimensional Galois representations, Duke Math. J. 149 (1) (2009), 37–116.Google Scholar
Humphreys, J. E., Modular representations of finite groups of Lie type, London Mathematical Society Lecture Note Series, Volume 326 (Cambridge University Press, Cambridge, 2006).Google Scholar
Jantzen, J. C., Representations of algebraic groups, second ed., Mathematical Surveys and Monographs, Volume 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21 (2) (2008), 513–546.CrossRefGoogle Scholar
Kisin, M., The Fontaine–Mazur conjecture for ${\mathrm{GL} }_{2} $, J. Amer. Math. Soc. 22 (3) (2009), 641–690.CrossRefGoogle Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 170 (3) (2009), 1085–1180.CrossRefGoogle Scholar
Kisin, M., The structure of potentially semi-stable deformation rings, Proceedings of the International Congress of Mathematicians, Volume II, pp. 294–311 (2010).Google Scholar
Labesse, J.-P., Changement de base CM et séries discrètes, preprint (2009).Google Scholar
Matsumura, H., Commutative ring theory, second ed., Cambridge Studies in Advanced Mathematics, Volume 8 (Cambridge University Press, Cambridge, 1989). Translated from the Japanese by M. Reid.Google Scholar
Paškūnas, V., Unicity of types for supercuspidal representations of ${\mathrm{GL} }_{N} $, Proc. Lond. Math. Soc. (3) 91 (3) (2005), 623–654.Google Scholar
Paškūnas, V., On the Breuil–Mézard conjecture (2012).Google Scholar
Savitt, D., On a conjecture of Conrad, Diamond, and Taylor, Duke Math. J. 128 (1) (2005), 141–197.Google Scholar
Shin, S. W., Galois representations arising from some compact Shimura varieties, Ann. of Math. (2) 173 (3) (2011), 1645–1741.Google Scholar
Snowden, A., On two-dimensional weight two odd representations of totally real fields, preprint (2009).Google Scholar
Taylor, R., On icosahedral Artin representations. II, Amer. J. Math. 125 (3) (2003), 549–566.CrossRefGoogle Scholar
Thorne, J., On the automorphy of $l$-adic Galois representations with small residual image, J. Inst. Math. Jussieu (2012), 1–66.Google Scholar