Research Article
On the radical of the group algebra of a p-nilpotent group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-123
-
- Article
-
- You have access
- Export citation
On a type of Sasakian space
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 508-510
-
- Article
-
- You have access
- Export citation
On the construction of the Kurosh lower radical class for associative rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 362-364
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 13 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 13 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
The deficiency and the multiplicator of finite nilpotent groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 124-128
-
- Article
-
- You have access
- Export citation
The subnormal structure of some classes of coluble groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-377
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 13 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 13 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On the semigroups of Fredholm mappings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 378-384
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 13 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 13 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
JAZ volume 13 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

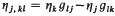

 is the conformal curvature tensor:
is the conformal curvature tensor: 