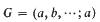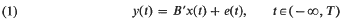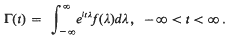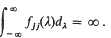Research Article
On normal complements to sections of finite groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-262
-
- Article
-
- You have access
- Export citation
Herbert Melvin Lieberstein
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
A class of simple groups with no doubly transitive representations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-145
-
- Article
-
- You have access
- Export citation
One-relator groups that are residually of prime power order
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-409
-
- Article
-
- You have access
- Export citation
The lateral completion of an arbitrary lattice group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-289
-
- Article
-
- You have access
- Export citation
Linear regression in continuous time
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-159
-
- Article
-
- You have access
- Export citation
Maximal right ideals of transformation near-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-412
-
- Article
-
- You have access
- Export citation
General-well-ordered sets
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-20
-
- Article
-
- You have access
- Export citation
On some two-dimensional cracks in linear isotropic elasticity
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-34
-
- Article
-
- You have access
- Export citation
Some results concerning a transformation semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-425
-
- Article
-
- You have access
- Export citation
On a class of finite groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-291
-
- Article
-
- You have access
- Export citation
A partial Baer *-semigroup of relations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-172
-
- Article
-
- You have access
- Export citation
Hereditarily universal sets
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 292-296
-
- Article
-
- You have access
- Export citation
Minimal arcs in metric spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 426-430
-
- Article
-
- You have access
- Export citation
Orthogonality relations on Abelian groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-179
-
- Article
-
- You have access
- Export citation
Independence results concerning Dedekindfinite sets
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-46
-
- Article
-
- You have access
- Export citation
On a generalization of the transformation semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-61
-
- Article
-
- You have access
- Export citation
Remarks on a class of 2-generator groups of deficiency zero
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-305
-
- Article
-
- You have access
- Export citation
Commutative distributive laws
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-195
-
- Article
-
- You have access
- Export citation
Ordering finite groups by involvement
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 431-436
-
- Article
-
- You have access
- Export citation